Izolita punkto
|
Por aliaj signifoj, bv. rigardi la apartigilan paĝon: Izolita punkto (kurbo) |
En topologio, punkto x de aro S estas nomita kiel izolita punkto, se tie ekzistas najbareco de x ne enhavanta aliajn punktojn de S.
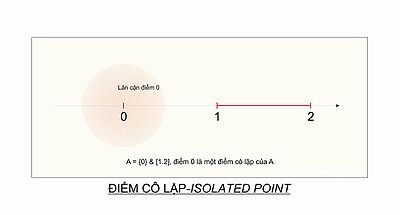
Aparte, en eŭklida spaco (aŭ en metrika spaco), x estas izolita punkto de S, se oni povas trovi malfermitan pilko ĉirkaŭ x kiu ne enhavas aliajn punktojn de S.
Ekvivalente, punkto x estas ne izolita se kaj nur se x estas limiga punkto.
Aro kiu estas farita nur de izolitaj punktoj estas nomita kiel diskreta aro . Diskreta subaro de eŭklida spaco estas kalkulebla; tamen, aro povas esti kalkulebla sed ne diskreta, ekzemple racionalaj nombroj.
Fermita aro sen izolitaj punktoj estas nomita kiel perfekta aro.
Ekzemploj redakti
Topologiaj spacoj en jenaj ekzemploj estas konsideritaj kiel subspacoj de la reela linio.
- Por aro , la punkto 0 estas izolita punkto.
![{\displaystyle S=\{0\}\cup [1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91214dd46eb1ba30f1b8ad577c4820f6985242e6)
- Por aro , ĉiu punktoj 1/k estas izolitaj punktoj, sed 0 estas ne izolita punkto ĉar estas aliaj punktoj en S tiel proksime al 0 kiel oni deziras.
- Aro N={0, 1, 2, ...} de naturaj nombroj estas diskreta aro.