Ordo-4 kvinlatera kahelaro
En geometrio, la ordo-4 kvinlatera kahelaro estas regula kahelaro de la hiperbola ebeno. Estas kvar kvinlateroj ĉirkaŭ ĉiu vertico. Ĝia simbolo de Schläfli estas {5,4}.
| Ordo-4 kvinlatera kahelaro | |
 Projekcio kiel diska modelo de Poincaré de la hiperbola ebeno. | |
| Speco | Regula kahelaro |
| Vertica figuro | 5.5.5.5 |
| Simbolo de Wythoff | 4 | 5 2 |
| Simbolo de Schläfli | {5,4} |
| Figuro de Coxeter-Dynkin | |
| Geometria simetria grupo | [5,4] |
| Duala | Ordo-5 kvadrata kahelaro |
| Bildo de duala | 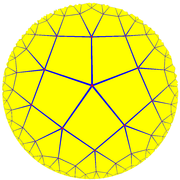
|
Vico de rilatantaj pluredroj kaj kahelaro redakti
La kvadrata kahelaro estas ero de vico de regulaj pluredroj kaj regulaj kahelaroj de la hiperbola ebeno kun verticaj figuroj (5n).
| Dekduedro (53) |
Ordo-4 kvinlatera kahelaro (54) |
Ordo-5 kvinlatera kahelaro (55) |
Noto ke en ĉi tiu vico forestas kahelaro de la eŭklida ebeno. Eŭklida ebeno ne povas esti kahelita nur per regulaj kvinlateroj.
Vidu ankaŭ redakti
Referencoj redakti
- Branko Grünbaum, Shephard G. C.. (1987) Tilings and Patterns - Kahelaroj kaj ŝablonoj. Novjorko: W. H. Freeman. ISBN 0-7167-1193-1.
Eksteraj ligiloj redakti
- Eric W. Weisstein, Hiperbola kahelaro en MathWorld.
- Eric W. Weisstein, Hiperbola disko de Poincaré en MathWorld.
- Galerio de hiperbolaj kaj sferaj kahelaroj Arkivigite je 2013-03-24 per la retarkivo Wayback Machine
- KaleidoTile 3 - kleriga programaro por krei sferajn, ebenajn kaj hiperbolajn kahelarojn
- Hiperbolaj ebenaj kahelaroj Arkivigite je 2011-09-27 per la retarkivo Wayback Machine
