Procezaŭtomacia algoritmo
Inĝenierarto > Procezaŭtomatigo >
La plej simpla regulleĝo estas la aktiva/malaktiva regulado. Ĉe aktiva/malaktiva regulado la fina regulelemento estas jen kompleta malferma/aktiva/maksimuma, jen kompleta ferma/malaktiva/minimuma, oni foje nomas ĝin regulado per ĉio aŭ neniu. Intervaloroj kaj interpozicioj, por la fina regulelemento ne ekzistas. Unu el malavantaĝoj kun la aktiva/malaktiva regulado estas ke la mekanika fina regulelemento povas eluziĝi tre rapide ĉar ĝi kontinue ŝaltas de malferma pozicio al ferma pozicio kaj reen. Por protekti la finan regulelementon oni ofte uzas mortan zonon, kiu estas zono limigita je maksimuma dezirata valoro kaj minimuma dezirata valoro. Dum la mezurita valoro restas inter la du limoj ne ekzistas ŝanĝojn en la regulada agado. Do se valvo estas fermita, ĝi restas fermita ĝis la mezurita valoro paŝas tra la minimuma limo. Tiam la valvo estos malfermita kaj restos malfermita ĝis la mezurita valoro paŝos iam tra la maksimuma limo. Estas multe da ekzemploj de aktiva/malaktiva regulado en ĉiutaga vivo. Hejtilado de domoj uzas ĝin, ankaŭ kiel fornoj, fridujoj kaj klimatizoj. La mezurita valoro ĉi tie estas, kompreneble, la temperaturo. La subestaranta figuro montras la agadon de regulila eligaĵa signalo kaj la mezurita valoro en aktivan/malaktivan reguladon kun "morta zono".
Intera valora regulado kaj PID algoritmo
redaktiPli fortaj reguladaj algoritmoj, kiuj permesas pli precizan reguladon kun malpli oscilado en la mezurata procezo, estas necesaj por diversaj procezaj aplikatoj. Ĉi tiuj algoritmoj kalkulas kompletan aron de reguladaj agadoj inter kompleta aktiva kaj kompleta malaktiva. Kompreneble necesas fina regulelemento, kiu povas enfokusiĝi interpoziciojn inter kompleta malfermita kaj kompleta fermita. La plej populara intera algoritmo estas la proporcia-integrala-diferenciala (PID) regulado, ĝi kalkulas interan valoran signalon surbaze la aktuala valoro de kontrolada eraro. La baza PID-algoritmo estas esprimata tiel:
u(t) = ubiaso + KCe(t) (proporcia) + KC / ΤI∫e(t)dt (integrala) + KCΤD de(t)/dt (diferenciala)
Kie:
u(t) = regulila eligaĵa signalo
ubiaso = regulila biaso aŭ nula valoro
e(t) = kontrolada eraro; e(t) = ydezirata valoro - y(t)
y(t) = mezurita procesa parametro
KC = regulila amplifika faktoro (proporcia adapta parametro)
ΤI = regulila remeta tempo (integrala adapta parametro)
ΤD = regulila diferenciala tempo (diferenciala adapta parametro)
La PID-algoritmo kontinue kalkulas kontrolajn agadojn u(t), kaj provas malgrandigi la kontroladan eraron al nulo. Kiel indikinte en la formulo, ĉiu termo laboras sendependita kaj kun malgranda diferenca intenco.
La proporcia termo kalkulas kontribuadon je la kontrolada agado surbaze la aktuala valoro de e(t) je la momento de mezurado. Nenia influado de antaŭaj mezuradoj estas inkluzivaj en la proporcia kalkulado.
La integrala termo kalkulas la kontinuajn sumojn aŭ akumulas e(t) je tempo. La integralo plue kreskas dum la kontrolado eraro estas pozitiva kaj komencas malplialtiĝi kiam la eraro estas negativa. Tiamaniere, la integralo fortiĝas sian influon kiam la pozitiva- aŭ la negativa eraro persistas dum kelka tempo.
La diferenciala termo plue kalkulas sumojn aŭ akumulas e(t) dum la tempo pasas. La diferenciala termo rigardas la deklivon de kontrolada erara ŝanĝo. Tiamaniere sian influon kreskas kiam la kontrolada erara ŝanĝo estas granda kaj provas bremsi tian movadon. Unu el la rezultoj estas, ke la diferencia agado amortizas osciladojn de la mezuritaproceza parametro.
Eblas fari la PID-algoritmon kiel nur partaj P, PI, PD aŭ kompleta PID formoj.
P-regulado
redaktiLa plej simpla regulado estas la P aŭ la proporcia regulado. La subestaranta figuro montras la agadon de P-regulado
La celo de la P-regulado estas egaligi la mezuritan procezan parametron al la dezirata valoro kaj tiamaniere eliminas la kontroladan eraron. Sed la P-regulado nur povas egaligi ĉi tiun parametron, kiam la dezirata valoro estas je la planita dezirata valoro. Kiam la dezirata valoro ne estas la planita, ofseto akazas. La P-regulada algoritmo kalkulas la regulilan eligaĵan signalon dum ĉiu cikla periodo, kiel:
u(t) = ubiaso + KCe(t)
ubiaso estas la regulila eligaĵan signalon necese por kontraŭstari la normalajn pertubojn. Ekzemple, veturilo havas deziratan valoron de rapideco ĉe 70 km/h. Ĉar y(t) = ydezirata valoro kaj e(t) = y(t) - ydezirata valoro, e(t) = 0, sekve u(t) = ubias. Se ubias = 0 u(t) = 0 ĉi tio indikas, ke la fluo de hejtilaĵo al la motoro ankaŭ estas 0. Sed tio estas absurdo, ĉar la veturilo devas venki minimume la froton. Kaj por venki la froton la motoro bezonas minimuman fluon de hejtilaĵo > 0. Ĉi tiu minimumo estas nomita la biaso.
Inversa agado, direkta agado kaj regula agado
Se la manipulita procezparametro altiĝas, kiam la regulila eligaĵa signalo altiĝas, la procezo estas definita
kiel procedo kun pozitiva amplifikada parametro KP . Ĉi tio signifas en la regulcirklo, kiam la
mezurita proceza parametro estas tro alta, komparinda kun la dezirata valoro, la regulado devas malaltigi la regulilan eligaĵan signalon por korekti la kontroladan eraron.
Ja:
e(t) = ydezirata valoro - y(t)
Ĉar y(t) (la mezurita proceza valoro) > ydezirata valoro sekvas e(t) < 0
Krome, la proporcia termo de algoritmo estas KCe(t)
La postulo estas, ke la regulado devas malaltigi la regulilan eligaĵan signalon, tiam:
KCe(t)<0
Ĉar e(t)<0 sekvas KC > 0
Do, kiam la procezo havas pozitivan KP kaj sekve pozitivan KC,la regulado devas havi inversan agadon.
La rezonado okaze de procezo kun negativa KP sekvas sammaniere.
Resumante:
KP kaj KC pozitiva → inversa agado
KP kaj KC negativa → direkta agado
Ofseto
Estas jam konata ke la regulila eligaĵa valoro u(t) = ubiaso + KCe(t) kie
e(t) = ydezirata valoro - y(t). Kiam y(t) estas stabila ĉe ydezirata valoro, e(t) estas stabila ĉe nulo. Kiam e(t) estas stabila ĉe nulo, u(t) estas stabila ĉe ubiaso. La aneksa valoro de ydezirata valoro ĉe ĉi tiu ubiaso estas la planita dezirata valoro, kiu estas trovinta per provi kelkajn diversajn valorojn. Kiam la dezirata valoro de operacio estas alia ke la planita dezirata valoro, estas necese ke ekzistas stabila stata eraro tiel, kiel u(t) povas havi alian valoron ke la ubiaso. La apogita valoro estas la ofseto (esperantigita vorto de la angla offset).
Proporcia zono
Kelkfoje por adapti reguladojn estas uzata la proporcia zono.
Ĝi estas difinita kiel:
PZ = 100 / KC
Kie la mezurita proceza parametro kaj la manipulita proceza parametro PZ estas esprimitaj de 0 ĝis 100%
PI-regulado
redaktiTiel, kiel la P-regulado, la PI-regulado kalkulas regulilan eligaĵan signalon al la fina regulelemento surbaze la adaptaj parametroj kaj la kontrolada eraro e(t). La aneksa formulo estas:
u(t) = ubiaso + KCe(t) + KC / ΤI∫e(t)dt
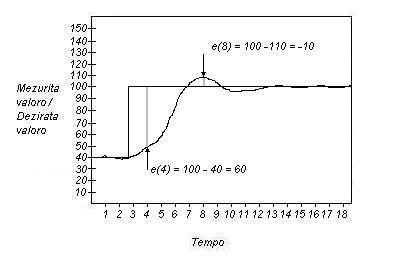
Sammaniere u(t) estas la regulila eligaĵa signalo, ubiaso estas la regulada biaso kaj KC estas la regulila amplifika faktoro (proporcia adapta parametro) de la regulado. La aldona parametro ΤI donas separatan pezon al la integrala termo kaj estas la nomita regulila remeta tempo. Ĉar ΤI estas la divizoro, pli malaltaj valoroj de remeta tempo havas pli altan pezon ol la integrala termo. La du unuaj termoj estas tiel, kiel en la formulo por la P-regulado. La integrala termo de PI-regulado estas aldona separata termo adiciinta al la ekvacio, kiu daŭre integralas aŭ sumas la kontroladan eraron je tempo. Sammaniere se ĉe la P-regulado, la proporcia termo de PI-regulado, KCe(t), adicias al aŭ subtrahas de ubiaso surbaze la diferenco inter la mezurita procezsa valoro kaj la dezirata valoro je ĉiu momento. Alivorte, la kontribuado de proporcia termo estas bazita sur e(t) je tempo t. Kiam e(t) plialtiĝis aŭ malplialtiĝis, la kvanton adiciinta al ubiaso kreskas aŭ malkreskas direkte kaj proporcie. La estinto kaj estanto ne havas influadon je la kalkuladon de proporcia termo. La subestaranta figuro montras ekzemplon de proporcia kalkulado.
Kontraŭe, la integrala termo de PI-regulado inkludas la historion de kontrolado eraro, tiamaniere atentu pri kiel longe kaj kiel fore la mezurita proceza parametro estis de la dezirata valoro je tempo. La integrala termo daŭre integralas aŭ sumas la historion de eraro. Do, eĉ tre malgranda eraro, se ĝi persistas, havos suman totalon, kiu kreskos je tempo kaj la integrala terma kontribuado adiciinta al ubiaso kreskos simile.
Kiel montrinta en la superestaranta figuro, la integralo plue kreskas se e(t) estas pozitiva, kaj malkreskas se e(t) estas negativa. Grave estas, kompreni ke la integrala termo povas havi restaĵan valoron post la transiro, eĉ kiam e(t) estas nulo. Estas konata, ke en multe da procezoj sub P-regulado okazas ofseton, se la dezirata valoro kaj/aŭ pertubo havas valoron alian, ol la planita, aŭ specifike, uzinta por difini ubiaso. Unu el avantaĝoj de PI-regulado estas, ke ĝi preskaŭ tute eliminas ofseton. Tio estas tiel, ĉar dum eraro restas (e(t) <> 0), la integrala termo kreskas aŭ malkreskas kaj kaŭzas ŝanĝon de la regulila eligaĵa valoro u(t). Ŝanĝo de u(t) nur haltas kiam y(t) egalas ydezirata valoro kaj sekve e(t) = 0 ... dum kelka tempo. Tiam la proporcia termo estas nulo kaj la integrala termo, kiel diskutinta, ankoraŭ havas restaĵan valoron. Ĉi tiu valoro, kiam adiciinta al ubiaso efektive kreas novan totalan biason kiu respondas al la nova operacia modo.
Kontinua (pozicia) kontraŭ diskreta (rapideca) formo
La kontinua formo de PI-regulado estas kiel konata:
u(t) = ubiaso + KCe(t) + KC / ΤI∫e(t)dt
Foje ĉi tiu formo estas nomita pozicia formo, ĉar la kalkulita u(t) estas specifa valoro en la zono de 0-100%. Kiam la fina regulelemento estas proceza valvo, la regulila eligaĵa valoro specifas la aktualan pozicion inter malfermita kaj fermita, kiun la valvo devas havi. La unua paŝo en derivi la diskreta formo estas kalkuli la diferencialon (al tempo t) de la kontinua formo.
du(t)/dt = dubiaso/dt + KCde(t)/dt + (KC/ΤI)e(t)
Ĉar la diferencialo de pozicio, du(t)/dt, estas rapideco, la diskreta formo de PI-regulado foje estas nomita la rapideca formo.
Ĉar ubiaso estas konstanta, dubiaso/dt = 0. Uzante finaj diferenciaj aproksimantoj por la kontinuaj diferencialoj la sekva formula estas atingita:
δ u / δ t = KC[(ei - ei-1)/ δ t] + KC ei/ΤI
Kie ei estas la aktuala kontrolada eraro kaj ei-1 la antaŭlasta. Kiam la regulilo difinas la eraron dum ĉiu periodo kun perioda tempo T = δt, la diskreta aŭ rapideca PI-regulado formo rezultas en:
δ u = KC[1 + T / ΤI]ei - KC ei-1
Ĉi tiu diskreta formo kalkulas ŝanĝon de la valvpozicio anstataŭ la pozicion mem. Kiom ajn la valpozicio estas, la δ u instruas la valvon pri la direkto kaj kiom ĝi devas iri. Dum la fina regulelemento ne atingas la maksimumon (100%) aŭ la minimumon (0%) kaj la kontinua kaj la diskreta formo kondutos sammaniere.
Remeta streĉado
Tiel longe kiel la kontrolado eraro persistas (ne estas nulo), la integrala termo en la pozicia formo plu kreskas. Se eraro estas sufiĉe granda kaj persistas sufiĉe longe, la kontribuado al ubias grandiĝos tiel, ke la fina regulelemento estos saturita aŭ
atingos fizikan limigon de kompletfermita aŭ kompletmalfermita. Kiam ĉi tiu ekstrema pozicio ne estas sufiĉa por nuligi la eraron, la matematika formulo permesas al la integrala termo kreski eĉ plue. Kiam la kalkulita u(t) trapasas la fizikan kapablecon de fina regulelemento, ĉar la integrala termo havas grandega valoro, ĉi tiu kondiĉo estas nomita streĉado. Ĉar streĉado estas ligita kun la integrala termo, ĉi tiu streĉado estas ofte referita kiel remeta streĉado.
Kiam la regulilo estas en ĉi tiu kondiĉo ĝi perdas la eblecon reguli la procezon. Nur se la eraro ŝanĝiĝos signon kaj komencos malkreski tiom, kiom la fina regulelemento ne estas saturita, la normala regulado povas komenci denove.
La diskreta (rapideca) formo neniam streĉas, ĉar la integrala termo estas forigita. Do, uzi la diskretan formon ne nur eliminas la biasan termon sed ankaŭ solvas la streĉadan problemon.
PID-regulado
redaktiLa PID regulado uzas, kompreneble, la totalan formon:
u(t) = ubias + KCe(t) + KC / ΤI∫e(t)dt + KCΤD de(t)/dt
La PI-parto estas jam priskribita superestarante. La diferenciala parto havas la adaptan parametron ΤD, kaj estas nomita
diferenciala tempo. Do ĝi havas unuon de tempo, ekzemple minuton, sekundon ktp, kaj ĝi estas ĉiam pozitiva. La superestaranta formo estas ofte nomita kiel ideala, malinteraga formo kaj ISA algoritmo. La diferenciala termo de formo (la D-agado) kalkulas la rapidecon per kiu la eraro ŝanĝiĝas je tempo. Eraro kiu ŝanĝiĝas rapide produktas grandan rapidecŝanĝon kaj produktas ĝin direkte.
La diferenciala kalkulado ne rigardas la signon de eraro nur la rapidecŝanĝon.
Ĉar:
de(t)/dt = d[ydezirata valoro - y(t)]/ dt
kaj ydezirata valoro estas konstanta, sekvas:
de(t)/dt = - dy(t)/dt .
Efektive, la diferencialo de eraro estas la diferencialo de mezurita proceza parametro.
La diferencialo de dy/dt estas kalkulita kiel la deklivo de y(t). Dume la mezurita proceza parametra ŝpuro altiĝas, la deklivo estas krutega kaj pozitiva, kiam ĝi malaltiĝas, ĝi estas negativa. Kiam y(t) trapasas de pinto al valon (kaj reciproke) ĝi estas nulo.
Tamen la ideala formo de PID-regulado havas malavantaĝon. Kiam la kontrolado eraro ŝanĝiĝas tre rapide, la ŝanĝo de valoro de y(t) povas esti, teorie, infinita. Praktike ĝi havos grandegan valoron esprimita kiel pinto en grafiko. Por eviti ĉi tiun fenomenon, praktike estas uzata la interaga formo de PID-regulado:
u(t) = ubias + [KC + KCΤD/ΤI]e(t) + KC / ΤI∫e(t)dt - KCΤDdy(t)/dt .
La agadoj de ambaŭ formoj estas samaj sed la interaga formo ne montras pintan agadon, tial ĝi estas praktike preferata.