Epicikloido

En geometrio, epicikloido estas ebena kurbo desegnita de fiksa punkto sur disko, kiu ruliĝas ĉirkaŭ kaj sur la ekstero de alia disko.

Epicikloido (ruĝa kurbo) kun $k=3$ (la rilatumo inter la radiusoj de la du diskoj) havas tri kuspojn

Difino

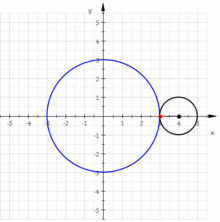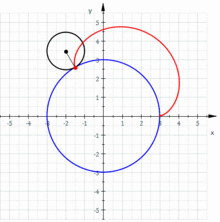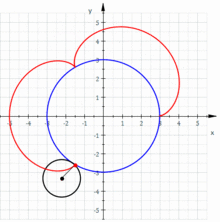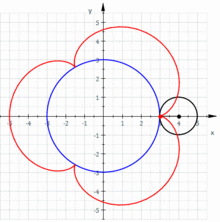
Konsideru eŭklidan ebenon $\mathbb {R} ^{2}$ kun karteziaj koordinatoj $(x,y)$. Supozu ke disko de radiuso $r$ ruliĝas sur disko de radiuso $kr$. Do, la epicikloido estas la kurbo difinita de la jenaj parametraj ekvacioj:

$x(t)=r(1+k)\cos t-r\cos((1+k)t)$

$y(t)=r(1+k)\sin t-r\sin((1+k)t)$

Propraĵoj

Se $k$ (la proporcio inter la radiusoj de la du diskoj) estas racionala nombro $k=p/q$, en kiu $p$ kaj $q$ estas nenulaj entjeroj primaj inter si, do la kurbo havas $p$ kuspojn.

Se $k$ estas neracionala, do la “kurbo” estas fakte densa subaro de la ringo de ena radiuso $kr$ kaj ekstera radiuso $(1+k)r$.

Historio

Epicikloido estas fama kurbo, kiu estis studata de klasikaj geometroj, interalie Dürer (1525), Desargues (1640), Huygens (1679), Leibniz, Newton (1686), de L’Hôpital (1690), Jacob Bernoulli (1690), la Hire (1694), Johann Bernoulli (1695), Daniel Bernoulli (1725), kaj Euler (1745, 1781).

La nomo devenas de la helenaj morfemoj antikve-greke ἐπῐ́, epí “sur”, antikve-greke κῠ́κλος, kúklos “ciklo”, kaj antikve-greke -ειδής, -eidḗs “adjektiviga sufikso”, kaj tiel signifas “surciklaĵo”, priskribante la manieron, kiel la kurbo estas difinita.

Vidu ankaŭ

• Cikloido
• Hipocikloido
• Kardioido

Eksteraj ligiloj

• Eric W. Weisstein, Epicycloid en MathWorld.
• Epicycloid (angle). MacTutor History of Mathematics Archive. Universitato de St. Andrews.