Lorenca forto

En fiziko, la lorenca forto aŭ forto de Lorentz estas forto aganta sur punkta ŝargo per elektromagnetaj kampoj. Ĝia valoro estas kalkulebla per la sekvanta ekvacio kun elektra kampo kaj elektromagneta indukto:

Irvojo de partikloj kun ŝargoj q de malaj signoj, sub influo de elektromagneta indukto B (perpendikle orientita rilate la ebenon de la desegno).

Fasko de elektronoj moviĝantaj cirkle, fare de magneta indukto. Viola lumo estas elsendita laŭ la elektronvojo, pro kolizioj de elektronoj kun gasmolekuloj en la bulbo.

$\mathbf {F} =q\,\mathbf {E} +q(\mathbf {v} \times \mathbf {B} ),$

kie

$\mathbf {F}$ estas la elektromagneta forto (mezurita en neŭtonoj),

$\mathbf {E}$ estas la elektra kampo (mezurita en voltoj je metroj),

$\mathbf {B}$ estas la magneta indukdenso (mezurita en tesloj),

$q\,$ estas la elektra ŝargo de la partiklo (mezurita en kulomboj),

$\mathbf {v}$ estas la estanta rapido de la partiklo (mezurita en metroj je sekundo),

$\times$ indikas la vektoran produton;

aŭ aliskribante per sekvantan ekvacio kun magneta vektora potencialo kaj elektra skalara potencialo:

$\mathbf {F} =q(-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}})+q(\mathbf {v} \times (\nabla \times \mathbf {A} )),$

kie

$\nabla$ kaj $\nabla \times$ estas respektive gradienta operatoro kaj kirla operatoro,

$\mathbf {A}$ kaj $\phi \,$ estas la magneta vektora potencialo kaj elektrostatika potencialo, respektive.

Notu ke ili estas vektoraj ekvacioj. Ĉiuj kvantoj skribitaj en grasaj literoj estas vektoroj (speciale F, E, v, B, A).

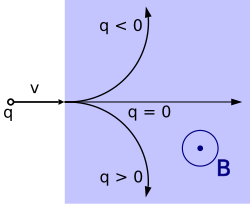
Pozitive ŝargita partiklo estos akcelita (aŭ malakcelita) laŭ la sama lineara direkto kiel la E kampo, sed devojiĝos laŭ kurbo en ebeno perpendikla al ambaŭ la rapida vektoro v kaj la magneta indukto B. Laŭ la regulo de la dekstra mano, se la polekso de la dekstra mano sekvos la vektoron v, kaj la indekso B, tiam la meza fingro indikos la direkton de F.

La unua produto F_el = q E nomiĝas la elektra forto, dum la dua produto F_mag = q v x B nomiĝas magneta forto .

La elektra forto akcelas la elementajn partiklojn en partiklaj akceliloj (linearaj aŭ cirklaj), kaj la magneta forto kurbigas la irvojon de la elementajn partiklojn en cirklaj partiklaj akceliloj (ekz. ciklotronoj, sinkrotonoj).

Laŭ kelkaj difinoj, la termino forto de Lorentz rilatas nur al la magneta forto:

$\mathbf {F} _{mag}=q(\mathbf {v} \times \mathbf {B} )$

kaj la tuta elektromagneta forto (inkluzivante la elektra forto) nomiĝas per alia ne klasika nomo. Sed pli komune, la termino forto de Lorentz rilatas al la tuta forto de la tuta ekvacio de Lorentz.

La magneta forta komponento de la lorenca forto aganta sur drato, en kiu trairas elektra kurento ankaŭ nomiĝas laplaca forto.

Laplaca forto

Pri alternativa reprezento de la regulo de la maldekstra mano.

La laplaca forto aŭ forto de Laplace estas la elektromagneta forto, kiu agas sur aron de ŝargitaj partikloj de konduktilo. Do estas rezultanto de la ago de la forto de Lorentz sur ĉiuj ŝargoj de grandaj objektoj (el multegaj atomoj). Oni povas diri, ke la laplaca forto estas lorenca forto sur konduktiloj.

Konsideru rigidan rektan draton submetita al konstanta magneta induko ${\vec {\mathbf {B} }},$. En tiu drato trairas elektraj ŝargoj kun konstanta rapido ${\vec {\mathbf {v} }}$, laŭ la dratdirekto; ilia daŭro $\mathbf {t}$ por irvoji la longon $\mathbf {\ell }$ de la drato sekvas la sekvantajn ekvaciojn laŭ la difino de la rapido:

${\vec {\mathbf {\ell } }}={\vec {\mathbf {v} }}\,t\,\,\,$,

kaj laŭ la difino de kurento $I$ (per la sumo de ĉiuj ŝargoj en la longo de la drato):

$\sum q=I\,t\,\,$;

do

$\sum q\,{\vec {\mathbf {v} }}=I\,{\vec {\mathbf {\ell } }}$,

tiel la sumo de la lorencaj fortoj estas:

${\vec {\mathbf {F} }}=\sum q\,{\vec {\mathbf {v} }}\times {\vec {\mathbf {B} }}\,$

kaj la ekvacio de la laplaca forto estas:

${\vec {\mathbf {F} }}=I\,\,{\vec {\mathbf {\ell } }}\times {\vec {\mathbf {B} }}\,\,.$

kie

${\vec {\mathbf {F} }}$ = forto, mezurita je neŭtonoj,

$\mathbf {I}$ = kurento en drato, mezurita je amperoj,

${\vec {\mathbf {B} }}$ = vektora magneta indukdenso, mezurita je tesloj,

$\times$ = vektora produto,

${\vec {\mathbf {\ell } }}$ = vektoro, kies valoro estas la longo de la drato (mezurita je metroj), kaj kies direkto laŭ la drato sekvas la vojon de pozitivaj ŝargoj (klasika difino de kurento, t.e. la efektiva kontraŭdirekto de elektronoj).

Alternative, kelkaj aŭtoroj skribas:

${\vec {\mathbf {F} }}=\mathbf {\ell } \,\,{\vec {\mathbf {I} }}\times {\vec {\mathbf {B} }}$

kie la vektora direkto estas ligita al kurento, anstataŭe al longo. La du ekvacioj validas same.

Se estas angulo $\alpha \,$ inter la drato kaj la magneta indukto, la modulo de la forto estas:l

$|{\vec {\mathbf {F} }}|=I\,|{\vec {\mathbf {\ell } }}|\,|{\vec {\mathbf {B} }}|\,\sin \alpha \,\;.$

Se la drato estas ne rekta, sed kurba, oni povas kalkuli la forton aplikante la formulon al ĉiuj elementaj partoj de la drato dℓ, kaj adiciante tiujn ĉi fortojn per integralo. La rezultanta forto sur senmova, rigida drato en kiu cirkulas kurento I estas:

${\vec {\mathbf {F} }}=I\int d{\vec {\boldsymbol {\ell }}}\times {\vec {\mathbf {B} }}({\boldsymbol {\ell }}\ )\;.$

Estus tordo, kaj pliaj aliaj efikoj, se la drato ne estus perfekte rigida.

Apliko pri la difino de la ampero

Sciante, ke la magnetaj flukslinioj estas cirklaj ĉirkaŭ konduktilo, per apliko de la ampera cirkvita leĝo, pri alia konduktilo lokata je distanco r, oni rajtas skribi:

$\int {{\vec {\mathbf {H} }}\mathrm {d} l}=I=2\pi r{\vec {\mathbf {H} }}\;;$

kaj plie en vakua medio

${\frac {\vec {\mathbf {B} }}{\mu _{0}}}={\frac {I}{2\pi r}}\;,$

kie $\mu _{0}=4\pi 10^{-7}$ estas la magneta konstanto, la magneta indukdenso en la loko de la dua konduktilo estas do:

${\vec {\mathbf {B} }}=I\;{\frac {\mu _{0}}{2\pi r}}={\frac {2\;10^{-7}}{r}}\;I\;,$

rezultas, ke, laŭ la laplaca forto

$|{\vec {\mathbf {F} }}|=2\;10^{-7}\;{\frac {\ell }{r}}\;|I|\,.$

Estas tiu formulo, kiu estas uzata por difini la bazon mezurunuon, ampero, de la internacia sistemo de unuoj, konsiderante kondiktilojn 1-m longajn, 1-m distanco inter ili kaj forto de 2. 10 ^-7 neŭtono.

Apliko pri la ampera leĝo

Alia apliko de tiu ekvacio estas la ampera forta leĝo, kiu priskribas kiel du dratoj trairataj de kurentoj altiriĝas aŭ repuŝiĝas unu al alia, ĉar ĉiu drato estas submetata al la forto de Lorentz de alia. Por pli informoj, vidu la artikolon pri ampera forta leĝo.

Vidu ankaŭ

• Ampera cirkvita leĝo
• Ampera forta leĝo
• Leĝo de Biot-Savart
• Kulomba leĝo
• André-Marie Ampère
• Pierre-Simon Laplace
• Hendrik Antoon Lorentz

Eksteraj ligiloj

• Video klariganta la movojn de ŝargitaj partikloj submetitaj al elektromagneta kampo