Rektigita 5-ĉelo
En geometrio, la rektigita 5-ĉelo estas konveksa uniforma plurĉelo. Kiel la nomo sugestas, ĝi povas esti farita per rektigo de la regula 5-ĉelo.
| Rektigita 5-ĉelo | |
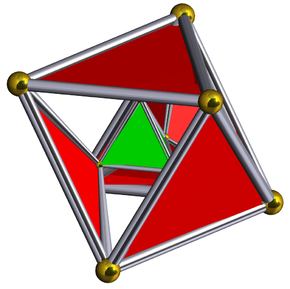 Figuro de Schlegel kun 5 kvaredraj ĉeloj montritaj. | |
| Speco | Uniforma plurĉelo |
| Vertica figuro | 2 kvaredroj (3.3.3) 3 okedroj (3.3.3) (triangula prismo) |
| Bildo de reto | 
|
| Simbolo de Schläfli | t1{3,3,3} |
| Figuro de Coxeter-Dynkin | |
| Simbolo de Bowers | Rap |
| Verticoj | 10 |
| Lateroj | 30 |
| Edroj | 30 trianguloj {3} |
| Ĉeloj | 5 kvaredroj (3.3.3) 5 okedroj (3.3.3) |
| Geometria simetria grupo | A4, [3,3,3] |
| Propraĵoj | Konveksa |



2 kvaredroj (3.3.3) kaj 3 okedroj (3.3.3))
Ĝi estas barita per 5 regulaj kvaredraj kaj 5 regulaj okedraj ĉeloj. Ĉiu latero estas ĉirkaŭita de unu kvaredro kaj du okedroj. Ĉiu vertico estas ĉirkaŭita de du kvaredroj kaj tri okedroj. Entute estas 30 triangulaj edroj, 30 lateroj kaj 10 verticoj.
Ĝi estas unu el tri duonregulaj plurĉeloj konsistantaj el ĉeloj de du aŭ pli multaj specoj kiuj estas platonaj solidoj (la aliaj du duonregulaj plurĉeloj estas la riproĉa 24-ĉelo kaj la rektigita 600-ĉelo).
La vertica figuro de la rektigita 5-ĉelo estas uniforma triangula prismo, formita de tri okedroj je la flankoj, kaj de du kvaredroj je la bazoj.
La rektigita 5-ĉelo estis esplorita de Thorold Gosset en lia papero de 1900.
Aliaj nomoj
redakti- Rektigita kvinĉelo
- Rektigita 4-simplaĵo
Bildoj
redakti
| Rektlinia sfera projekcio centrita je okedro | Orta projekcio de dekliva direkto kun stelokvinlatera simetrio. |
Vidu ankaŭ
redaktiReferencoj
redakti- Thorold Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions - Pri la regula kaj duonregulaj figuroj en spaco de n dimensioj, Messenger of Mathematics - Kuriero de matematiko, Macmillan, 1900
Eksteraj ligiloj
redakti- Rektigita 5-ĉelo - datumoj kaj bildoj
