Entutotranĉita 120-ĉelo

En geometrio, la entutotranĉita 120-ĉelo aŭ entutotranĉita 600-ĉelo estas konveksa uniforma plurĉelo. Kiel la nomoj sugestas, ĝi povas esti farita per entutotranĉo de la regula 120-ĉelo aŭ per entutotranĉo de la regula 600-ĉelo.

Entutotranĉita 120-ĉelo
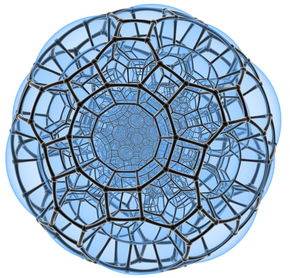Rektlinia sfera projekcio centrita je senpintigita dudek-dekduedro
Speco	Uniforma plurĉelo
Vertica figuro	Nememspegulsimetria skalena kvaredro
Simbolo de Schläfli	t0,1,2,3{3,3,5}
Simbolo de Bowers	Gidpixhi
Verticoj	14400
Lateroj	28800
Edroj	17040 tuteca: 10800 kvadratoj {4}, 4800 seslateroj {6} 1440 deklateroj {10}
Ĉeloj	Entute 2640: 120 senpintigitaj dudek-dekduedroj (4.6.10) 600 senpintigitaj okedroj (4.6.6) 720 deklateraj prismoj (4.4.10) 1200 seslateraj prismoj (4.4.6)
Geometria simetria grupo	H4, [3,3,5]
Propraĵoj	Konveksa

Ĝi estas komponita el 2640 ĉeloj: 120 senpintigitaj dudek-dekduedroj, 600 senpintigitaj okedroj, 720 deklateraj prismoj kaj 1200 kvinlateraj prismoj.

Ĝi ankaŭ havas 14400 verticojn, 28800 laterojn kaj 17040 edrojn, kaj estas la plej granda je kvanto de la eroj konveksa uniforma plurĉelo.

La verticoj kaj lateroj formas grafeon de Cayley de la grupo de Coxeter H₄

Vidu ankaŭ

• Uniforma plurĉelo
• 120-ĉelo
• 600-ĉelo
• Entutotranĉita 5-ĉelo
• Entutotranĉita 4-hiperkubo (aŭ entutotranĉita 16-ĉelo)
• Entutotranĉita 24-ĉelo

Referencoj

• Kalejdoskopoj: Elektitaj skriboj de H.S.M. Coxeter, redaktita de F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Papero 22) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Papero 23) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj II, [Math. Zeit. 188 (1985) 559-591]
  • (Papero 24) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj III, [Math. Zeit. 200 (1988) 3-45]
• John Horton Conway kaj Michael Guy: Kvar-dimensiaj arĥimedaj hiperpluredroj, Paperoj de la Kolokvo sur Konvekseco je Kopenhago, paĝo 38 kaj 39, 1965
• Norman Johnson: La teorio de uniformaj hiperpluredroj kaj kahelaroj, Ph.D. Disertaĵo, Universitato de Toronto, 1966

Eksteraj ligiloj

• Entutotranĉita 120-ĉelo (46) en konveksaj uniformaj plurĉeloj de George Olshevsky
• Entutotranĉita 120-ĉelo (entutotranĉita 600-ĉelo) en arĥimedaj hiperpluredroj en R⁴ de Marco Möller
• Fotoj Arkivigite je 2007-08-14 per la retarkivo Wayback Machine de modelo de Zome de entutotranĉita 120-ĉelo. La unua plena fizika modelo de 3D projekcio de la entutotranĉita 120-ĉelo estis konstruita per teamo kondukita de Daniel Duddy kaj David Richter en la 9-a de aŭgusto 2006 per sistemo Zome en la londona Knowledge Lab por la 2006-a Konferenco de Pontoj.