Riproĉa dekduedro
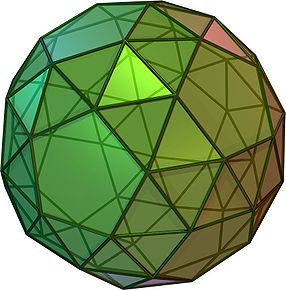
La riproĉa dekduedro, aŭ riproĉa dudek-dekduedro, estas pluredro, arĥimeda solido.
| Riproĉa dekduedro | |

| |
| |
| Klaku por rigardi turnantan bildon | |
| Speco | nememspegulsimetria |
| Vertica figuro | 3.3.3.3.5 |
| Bildo de vertico | 
|
| Bildo de reto | 
|
| Simbolo de Wythoff | | 2 3 5 |
| Simbolo de Schläfli | |
| Figuro de Coxeter-Dynkin | |
| Indeksoj | U29 C32 W18 |
| Simbolo de Bowers | Snid |
| Verticoj | 60 |
| Lateroj | 150 |
| Edroj | 92 |
| Edroj detale | (20+60){3}+12{5} |
| χ | 2 |
| Geometria simetria grupo | Mi |
| Duala | Kvinlatera sesdekedro |
| Bildo de duala | 
|
La riproĉa dekduedro havas 92 edrojn el kiuj 12 estas kvinlateroj kaj la restaj 80 estas egallateraj trianguloj. Ĝi ankaŭ havas 150 laterojn kaj 60 verticojn. Ĝi havas du diversajn formoj, kiuj estas spegulaj bildoj unu de la alia.
La riproĉa dekduedro povas esti konstruita per preno la dek du kvinlateraj edroj de la dekduedro kaj distirado ilin eksteren malmulte tiel ke ili jam ne intertuŝu. Tiam donu al ĉiu el ili malgrandan turnon ĉirkaŭ akso orta al la edra ebeno kaj estanta tra la centro. Ili ĉiuj devas esti turnitaj je la sama angulo kaj en la sama direkto - laŭhorloĝnadle aŭ mallaŭhorloĝnadle, se rigardi deekstere. Tiam la spaco inter la kvinanguloj povas esti plenigita per trianguloj. Se ĉiuj operacioj estas faritaj je vera grado la trianguloj estos egallateraj kaj la rezultanta pluredro estos unuforma.
 Dekduedro |
 Rombo-dudek-dekduedro |
Karteziaj koordinatoj redakti
Karteziaj koordinatoj de verticoj de riproĉa dekduedro estas ĉiuj paraj permutoj de
- (±2α, ±2, ±2β),
- (±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1)),
- (±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ)),
- (±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)),
- (±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1)),
kun para kvanto de plusoj, kie
- α = ξ-1/ξ
kaj
- β = ξτ+τ2+τ/ξ,
kie τ = (1+√5)/2 estas la ora proporcio kaj ξ estas la reela solvaĵo al ξ3-2ξ=τ, kiu estas
aŭ proksimume 1,7155615.
Vico de rilatantaj pluredroj kaj kahelaroj redakti
La riproĉa dekduedro estas ero de vico de riproĉigitaj regulaj pluredroj kaj regulaj kahelaroj de la eŭklida kaj hiperbola ebenoj kun verticaj figuroj (3.3.3.3.n).
| Dudekedro (3.3.3.3.3) |
Riproĉa kubo (3.3.3.3.4) |
Riproĉa dekduedro (3.3.3.3.5) |
| Riproĉa seslatera kahelaro 3.3.3.3.6 |
Riproĉa ordo-3 seplatera kahelaro (3.3.3.3.7) |
Riproĉa ordo-3 oklatera kahelaro (3.3.3.3.8) |
Vidu ankaŭ redakti
Referencoj redakti
- Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)
Eksteraj ligiloj redakti
- Eric W. Weisstein, Riproĉa dekduedro en MathWorld.
- La unuformaj pluredroj
- Virtualaj realaj pluredroj - la enciklopedio de pluredroj
- Drata modelo Arkivigite je 2007-09-28 per la retarkivo Wayback Machine

