Ora proporcio
La ora proporcio (latine sectio aurea) estas rilato inter du nombroj, plej ofte distancoj, rigardata en la arto kaj arkitekturo kiel centra nocio pri estetiko kaj perfekta harmonio. Plue la ora proporcio aperadas ankaŭ en la naturo kaj havas interesajn matematikajn ecojn.
La oran nombron oni renkontas en la naturo, en arto ktp, sed unuavice en matematiko, kaj ĉefe ĝiajn matematikajn ecojn oni konsideras laŭ moderna vidpunkto, komencante per geometrio, kie ĝi rolas en pristudo de plurlateroj kaj pluredroj, sed ankaŭ en aritmetiko, kie, lige kun la vico de Fibonacci, ĝi havas unikajn ecojn. Fakuloj profunde traktas la diversajn matematikajn ecojn kaj ligitajn demandojn, ekzemple kiuj regulaj plurlateroj krom la kvinlateroj estas desegneblaj per liniilo kaj cirkelo, kial por ĉiu reela nombro ekzistas frakcioj almenaŭ tiom proksimaj al la nombro kiel por la ora nombro (do ĝi estas la plej malbona rilate la eblon trovi proksimajn frakciojn).[1]
Ora sekco estas divido de difinita distanco je du partoj, per kiu la rilato de la malgranda parto al la granda estas la sama kiel la rilato de la granda al la tuto. Se la tuta longo estas a kaj la pli granda parto estas x, tiam la pli malgranda parto estas a – x. La proporcio estas do (a – x) : x = x : a.
La bazo de la ora proporcio estas la nombro fi (Φ, φ) :
-
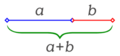
Ora proporcio sur linio
-
Aproksimo de ora spiralo per kvadratoj, oraj ortanguloj kaj cirkelo. Ora spiralo estas speciala tipo de logaritma spiralo.
-
Konstruado de ora ortangulo per liniilo kaj cirkelo.
Kalkulado
redakti| Listo de nombroj – Neracionalaj nombroj ζ(3) – √2 – √3 – √5 – φ – α – e – π – δ | |
| En duuma sistemo | 1.1001111000110111011... |
| En dekuma sistemo | 1.6180339887498948482... |
| En deksesuma sistemo | 1.9E3779B97F4A7C15F39... |
| kiel senfina frakcio | |
| kiel senfina radiko | |
| Algebra nombro | |
Du kvantoj pozitivaj a kaj b estas en la ora proporcio , se
Ĉi tiu ekvacio difinas senambigue la nombron
La ekvacio dekstra montras, ke , kion ni substituu en la maldekstra parto:
Oni povas elimini b-on, kio donas
Multiplikante ambaŭ flankojn per kaj transŝovante terminojn, ni ricevas
La nura pozitiva solvo de ĉi tiu kvadrata ekvacio estas
Ora vico
redakti| 4 | ≈ 6,854 | |
| 3 | ≈ 4,236 | |
| 2 | ≈ 2,618 | |
| 1 | ≈ 1,618 | |
| 0 | = 1,000 | |
| −1 | ≈ 0,618 | |
| −2 | ≈ 0,382 | |
| −3 | ≈ 0,236 | |
| −4 | ≈ 0,146 |
Pri donita nombro , konstruu sekvencon por . Ĉi tiu vico havas la proprecon, ke ĉiu tri sinsekvaj termoj kongruas al oraj proprcioj, tio estas:
- kie por ĉiuj
Ĉi tiu vico grave rolas en la teorio de proporcioj en arto kaj arĥitekturo, ĉar por donita longo aliaj harmoniaj aspektoj povas esti generitaj. Kiel rezulto, objektoj de tre malsamaj dimensioj, kiel fenestro kaj larĝa ĉambro, povas esti rilatigitaj per la ora proporcio kaj krei tutan serion de harmoniaj dimensioj.
Valoras noti sur la apuda tabelo, ke pri pri la tri elementoj de la vico kaj , la diferenco inter ili estas entjero.
Vidu ankaŭ
redaktiNotoj
redakti- ↑ François Lo Jacomo, La ora nombro, en IKU-libro de 2020, Internacia Kongresa Universitato, Universala Esperanto-Asocio. Red. Anna Striganova, Dmitrij Ŝevĉenko, Amri Wandel, Eldonejo «Impeto», Tutmonde, 73-a sesio, 01a — 08a de aŭgusto 2020, 106 pp. pp. 20-35. ISBN 978-5-7161-0314-6