Senpintigita 120-ĉelo

En geometrio, la senpintigita 120-ĉelo estas konveksa uniforma plurĉelo. Kiel la nomo sugestas, ĝi povas esti farita per tranĉo de verticoj de la regula 120-ĉelo.

Senpintigita 120-ĉelo
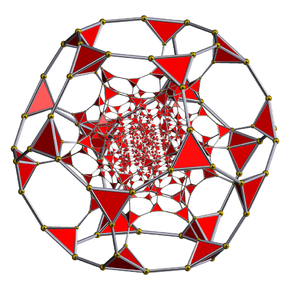Figuro de Schlegel kun kvaredraj ĉeloj montritaj
Speco	Uniforma plurĉelo
Vertica figuro	Egallatera triangula piramido (malregula kvaredro) (3 senpintigitaj dekduedroj kaj unu kvaredro kuniĝas je ĉiu vertico).
Bildo de vertico	Bildo de vertico
Simbolo de Schläfli	t0,1{5,3,3}
Figuro de Coxeter-Dynkin
Verticoj	2400
Lateroj	4800
Edroj	2400 trianguloj 720 deklateroj
Ĉeloj	600 kvaredroj (3.3.3) 120 senpintigitaj dekduedroj (3.10.10)
Geometria simetria grupo	H4, [3,3,5]
Propraĵoj	Konveksa

La senpintigita 120-ĉelo havas 120 senpintigitajn dekduedrajn kaj 600 kvaredrajn ĉeloj. Ĝi havas 3120 edrojn: 2400 triangulojn kaj 720 deklaterojn. Ĝi havas 4800 laterojn de du specoj: 3600 estas komunigitaj de tri senpintigitaj dekduedroj kaj 1200 estas komunigitaj de du senpintigitaj dekduedroj kaj unu kvaredro. Ĉiu vertico havas 3 senpintigitaj dekduedroj kaj unu kvaredro ĉirkaŭ ĝi. La vertica figuro estas egallatera triangula piramido.

Bildoj

Reta hiperpluredro	Centra parto de rektlinia sfera projekcio centrita je senpintigita kvaredro

Vidu ankaŭ

• Senpintigita 5-ĉelo
• Senpintigita 4-hiperkubo
• Senpintigita 16-ĉelo
• Senpintigita 24-ĉelo
• Senpintigita 600-ĉelo

Referencoj

• Kalejdoskopoj: Elektitaj skriboj de H.S.M. Coxeter, redaktita de F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Papero 22) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Papero 23) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj II, [Math. Zeit. 188 (1985) 559-591]
  • (Papero 24) H.S.M. Coxeter, Regulaj kaj duonregulaj hiperpluredroj III, [Math. Zeit. 200 (1988) 3-45]
• John Horton Conway kaj Michael Guy: Kvar-dimensiaj arĥimedaj hiperpluredroj, Paperoj de la Kolokvo sur Konvekseco je Kopenhago, paĝo 38 kaj 39, 1965
• Norman Johnson: La teorio de uniformaj hiperpluredroj kaj kahelaroj, Ph.D. Disertaĵo, Universitato de Toronto, 1966

Eksteraj ligiloj

• Senpintigita 120-ĉelo (36) en konveksaj uniformaj plurĉeloj de George Olshevsky
• Senpintigita 120-ĉelo en arĥimedaj hiperpluredroj en R⁴ de Marco Möller