5-hiperkubo

En geometrio, 5-hiperkubo estas regula 5-hiperpluredro, kvin-dimensia hiperkubo kun 32 verticoj, 80 lateroj, 80 kvadrataj edroj, 40 kubaj ĉeloj, kaj 10 4-hiperkubaj 4-hiperĉeloj.

5-hiperkubo
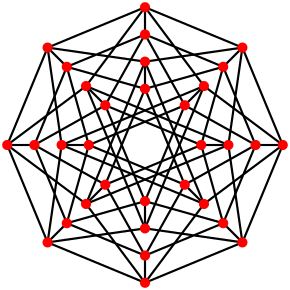Grafeo de verticoj kaj lateroj
Speco	Regula 5-hiperpluredro Hiperkubo
Vertica figuro	Kvinĉelo
Simbolo de Schläfli	{4,3,3,3}
Figuro de Coxeter-Dynkin
Verticoj	32
Lateroj	80
Edroj	80 kvadratoj
Ĉeloj	40 kuboj
4-hiperĉeloj	10 4-hiperkuboj
Geometria simetria grupo	B5, [3,3,3,4]
Propraĵoj	konveksa
Duala	5-kruco-hiperpluredro

Ĝi povas ankaŭ nomiĝi regula 10-5-hiperpluredro, ĉar ĝi estas regula, 5-dimensia kaj konsistas el 10 facetoj.

Ĝi estas parto de malfinia hiperpluredra familio de hiperkuboj. La duala hiperpluredro de 5-hiperkubo estas 5-kruco-hiperpluredro, kiu estas ero de la alia malfinia hiperpluredra familio de kruco-hiperpluredroj.

Se apliki alternadan operacion al 5-hiperkubo, do forviŝi alternajn verticojn de la 5-hiperkubo, rezultiĝas uniforma hiperpluredro, e5 hiperpluredro, kiu estas ero de malfinia hiperpluredra familio de la duonverticaj hiperkuboj.

Karteziaj koordinatoj

Karteziaj koordinatoj de verticoj de 5-hiperkubo centrita je la fonto kun latera longo 2 estas

(±1,±1,±1,±1,±1)

kaj la eno de ĝi konsistas el ĉiuj punktoj (x₀, x₁, x₂, x₃, x₄) tiaj ke -1 < x_i < 1.

Bildoj

Dratoframa (orta projekcio)

Perspektiva projekcio 3D al 2D de rektlinia sfera projekcio 4D al 3D de figuro de Schlegel 5D al 4D.

Vidu ankaŭ

• Aliaj 5-hiperpluredroj:
  • Regulaj
    • 5-simplaĵo - {3,3,3,3}
    • 5-kruco-hiperpluredro - {3,3,3,4}
  • Neregulaj
    • 5-duonvertica hiperkubo
• Aliaj hiperkuboj:
  • Kvadrato {4}
  • Kubo {4,3}
  • 4-hiperkubo {4,3,3}
  • 5-hiperkubo {4,3,3,3}
  • 6-hiperkubo {4,3,3,3,3}
  • 7-hiperkubo {4,3,3,3,3,3}
  • 8-hiperkubo {4,3,3,3,3,3,3}
  • ...

Referencoj

• H. S. M. Coxeter, Regular Polytopes - Regulaj hiperpluredroj, 3-a. red., Dover Publications, 1973. ISBN 0-486-61480-8, p.296, Tabelo I (iii): Regulaj hiperpluredroj, tri regulaj hiperpluredroj en n dimensioj (n>=5)

Eksteraj ligiloj

• Eric W. Weisstein, Hiperkubo en MathWorld.
• George Olshevsky, Mezura hiperpluredro en Glossary for Hyperspace.
• Multdimensia glosaro: hiperkubo de Garrett Jones