Unuforma hiperpluredro
En geometrio, unuforma hiperpluredro estas vertico-transitiva hiperpluredro farita el unuformaj hiperpluredraj facetoj. Unuforma hiperpluredro devas ankaŭ havi nur regulajn plurlaterajn edrojn.
Samformeco estas ĝeneraligo de la pli malnova kategorio duonregula, sed ankaŭ inkluzivas la regulajn hiperpluredrojn. Plu, nekonveksaj regulaj edroj kaj verticaj figuroj (stelaj plurlateroj) estas permesitaj, kio grande elvolvi la aron de konsiderataj formoj. Severa difino postulas ke unuformaj hiperpluredroj estu finiaj. Pli ĝeneraliga difino permesas al unuformaj kahelaroj de eŭklida spaco kaj hiperbola spaco al esti konsiderataj kiel hiperpluredroj.
Proksime ĉiuj unuformaj hiperpluredroj povas esti generitaj per konstruo de Wythoff kaj prezentitaj per figuro de Coxeter-Dynkin.
Operacioj
redaktiAnkaŭ iuj operacioj povas esti uzataj por konstrui unuformajn hiperpluredrojn.
Rektigoj
redaktiRegula n-dimensia hiperpluredro havas n gradojn de rektigo, kiu produktas unuforman rezulton.
- La nula rektigo estas la originala formo.
- La unua rektigo malpligrandigas laterojn al la novaj verticoj.
- La dua rektigo malpligrandigas edrojn al la novaj verticoj.
- La tria rektigo ĉeloj al la novaj verticoj.
- ...
- La n-a rektigo estas la duala hiperpluredro.
Etendita simbolo de Schläfli kun sola suba indico povas esti uzata por priskribi rektigitajn formoj. La k-a rektigo estas skribata kiel tk{p1, p2, ..., pn-1}
Tranĉoj
redaktiRegulaj n-hiperpluredroj havas n-1 variantojn de tranĉoj kiuj povas esti aplikitaj en ĉiu kombinaĵo, kaj kiu povas krei novaj unuformaj hiperpluredroj. Tiel entute estas 2n-1 variantoj kune kun la fonta formo.
Apartaj tranĉoj estas:
- Senpintigo - aplikebla al plurlateroj kaj pli altaj
- Laterotranĉo - aplikebla al pluredroj kaj pli altaj
- Edrotranĉo - aplikebla al plurĉeloj kaj pli altaj
- Ĉelotranĉo - aplikebla al 5-hiperpluredroj kaj pli altaj
- ...
Se ĉiuj tranĉoj estas aplikita senprokraste la operacio povas esti pli ĝenerale (nomita, vokis) entutotranĉo.
Etendita simbolo de Schläfli kun pluraj subaj indicoj povas esti uzata por priskribi tranĉitajn formoj. En ĝi nepre estas indico 0 kaj la aliaj en ajnaj kombinaĵoj. Ekzemple edroverticotranĉo estas t0, 1, 3{p1, p2, ..., pn-1}.
Rektigoj kaj tranĉoj
redaktiRektigoj kaj tranĉoj povas esti konsiderataj kune kaj eble aplikataj kune.
Etendita simbolo de Schläfli kun pluraj subaj indicoj povas esti uzata por priskribi ĉi tiajn formoj. En ĝi nepre estas almenaŭ unu indico. Tiel entute estas 2n-1 variantoj kune kun la fonta formo.
Apliko de la operacioj estas ekvivalenta al dismeto de ringitaj verticoj en figuro de Coxeter-Dynkin.
Alternado
redaktiAlternado estas operacio kiu forprenas alternajn verticojn de hiperpluredro. Ĝi povas esti farira nur se ĉiu edro havas paran kvanton de verticoj.
Riproĉigo estas alternado aplikita al entutotranĉita hiperpluredro; la rezulto de entutotranĉo ĉiam havas paran kvanton de verticoj ĉe ĉiu edro.
La rezultanta hiperpluredro ĉiam povas esti konstruita, sed estas ne nepre memspegulsimetria. Ankaŭ, la rezulto estas ĝenerale ne unuforma, sed ĝi ofte povas esti misformigita tiel ke ĝi ekestu unuforman.
Klasoj de hiperpluredroj laŭ dimensio
redakti- Unuformaj plurlateroj
- Konveksaj
- Malfinia aro de regulaj plurlateroj
- Nekonveksaj
- Malfinia aro de stelaj plurlateroj (unu por ĉiu racionala nombro pli granda ol 2).
- Konveksaj
- Unuformaj pluredroj
- Konveksaj
- 5 konveksa regulaj (platonaj solidoj)
- 13 konveksa duonregulaj (arĥimedaj solidoj)
- Malfinia aro de duonregulaj prismoj (unu por ĉiu konveksa regula plurlatero)
- Malfinia aro de duonregulaj kontraŭprismoj (unu por ĉiu konveksa regula plurlatero)
- Nekonveksaj
- 4 nekonveksaj regulaj (pluredroj de Keplero-Poinsot)
- 53 aliaj nekonveksaj
- Malfinia aro de nekonveksaj unuformaj prismoj (unu por ĉiu regula stelo (figuro))
- Malfinia aro de nekonveksaj unuformaj kontraŭprismoj (unu por ĉiu neentjera racionala nombro pli granda ol 3/2)
- Konveksaj
- Unuformaj plurĉeloj
- Konveksaj
- 6 konveksaj regulaj plurĉeloj
- 41 neprismaj konveksaj unuformaj plurĉeloj;
- 18 konveksaj hiperprismoj bazita sur la platonaj kaj arĥimedaj solidoj (inkluzivante la kubo-prismon, kiu estas la regula 4-hiperkubo);
- Malfinia aro de hiperprismoj bazitaj sur la konveksaj kontraŭprismoj;
- Malfinia aro de konveksaj duprismoj - karteziaj produtoj de du konveksaj regulaj plurlateroj
- Nekonveksaj
- 10 nekonveksaj regulaj plurĉeloj (plurĉeloj de Schläfli-Hess)
- 57 nekonveksaj hiperprismoj bazitaj sur la nekonveksaj unuformaj pluredroj;
- Nekonata kvanto de nekonveksaj neprismaj unuformaj plurĉeloj (pli ol mil jam estas trovitaj);
- Malfinia aro de hiperprismoj bazita sur la nekonveksaj kontraŭprismoj;
- Malfinia aro de nekonveksaj duprismoj - karteziaj produtoj de konveksa regula plurlatero
- Konveksaj
kaj stela plurlatero.
- Malfinia aro de nekonveksaj duprismoj - karteziaj produtoj de du stelaj plurlateroj.
Pli alte dimensiaj unuformaj hiperpluredroj estas ne plene sciata. Plej parto povas esti generita per konstruo de Wythoff aplikita al la regulaj formoj.
Familioj de konveksaj unuformaj hiperpluredroj
redaktiRegulaj n-hiperpluredraj familioj estas la simplaĵoj, hiperkuboj, kaj kruco-hiperpluredroj.
La duonvertica hiperkuba familio, derivita de la hiperkuboj per forprenado de alternaj verticoj, inkluzivas la regulan kvaredron derivitan de la kubo kaj la regulan 16-ĉelo derivita de la 4-hiperkubo. Pli altaj membroj de la familio estas unuformaj sed ne regulaj, komence kun 5-duonvertica hiperkubo derivita de la 5-hiperkubo.
Estas ankaŭ familioj de unuformaj k21 hiperpluredroj, unuformaj 2k1 hiperpluredroj, unuformaj 1k2 hiperpluredroj.
Notu, ke la familioj en ĉi tiu senco ne estas apartaj, iuj formoj apartenas al kelkaj familioj.
Familioj de konveksaj unuformaj hiperpluredroj laŭ grupoj de Coxeter
redaktiFamilioj de konveksaj unuformaj hiperpluredroj estas difinitaj per grupoj de Coxeter. Prismoj estas difinitaj per produtoj de ĉi tiuj grupoj.
Listo de la familioj, supren ĝis 8-hiperpluredroj, estas donita pli sube.
La figuro de Coxeter-Dynkin estas donita por la unua formo en ĉiu familio. Ĉiu kombinaĵo de ringoj, kun ĉiu prisma grupo havanta almenaŭ unu ringon, produktas unuforman hiperpluredron.
- A1: [ ]
 - streko
- streko
- A1: [ ]
- A6:[3, 3, 3, 3, 3]











- C6:[4, 3, 3, 3, 3]











- B6: [33, 1, 1]









- E6: [32, 2, 1]









- A5xA1: [3, 3, 3, 3] x [ ]











- C5xA1:[4, 3, 3, 3] x [ ]











- B5xA1: [32, 1, 1] x [ ]









- A4xD2p: [3, 3, 3] x [p]











- C4xD2p: [4, 3, 3] x [p]











- F4xD2p: [3, 4, 3] x [p]











- G4xD2p: [5, 3, 3] x [p]











- B4xD2p: [31, 1, 1] x [p]







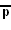

- A3xA3: [3, 3] x [3, 3]











- A3xC3: [3, 3] x [4, 3]











- A3xG3: [3, 3] x [5, 3]











- C3xC3: [4, 3] x [4, 3]











- C3xG3: [4, 3] x [5, 3]











- G3xA3: [5, 3] x [5, 3]











- A3xD2pxA1: [3, 3] x [p] x [ ]











- C3xD2pxA1: [4, 3] x [p] x [ ]











- G3xD2pxA1: [5, 3] x [p] x [ ]











- D2pxD2qxD2r: [p] x [q] x [r]











- A6:[3, 3, 3, 3, 3]
- A7: [36]













- C7: [4, 35]













- B7: [34, 1, 1]











- E7: [33, 2, 1]











- A6xA1: [35] x [ ]













- C6xA1: [4, 34] x [ ]













- B6xA1: [33, 1, 1] x [ ]











- E6xA1: [32, 2, 1] x [ ]











- A5xD2p: [3, 3, 3] x [p]













- C5xD2p: [4, 3, 3] x [p]













- B5xD2p: [32, 1, 1] x [p]









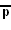

- A4xA3: [3, 3, 3] x [3, 3]













- A4xC3: [3, 3, 3] x [4, 3]













- A4xG3: [3, 3, 3] x [5, 3]













- C4xA3: [4, 3, 3] x [3, 3]













- C4xC3: [4, 3, 3] x [4, 3]













- C4xG3: [4, 3, 3] x [5, 3]













- G4xA3: [5, 3, 3] x [3, 3]













- G4xC3: [5, 3, 3] x [4, 3]













- G4xG3: [5, 3, 3] x [5, 3]













- F4xA3: [3, 4, 3] x [3, 3]













- F4xC3: [3, 4, 3] x [4, 3]













- F4xG3: [3, 4, 3] x [5, 3]













- B4xA3: [31, 1, 1] x [3, 3]











- B4xC3: [31, 1, 1] x [4, 3]







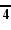



- B4xG3: [31, 1, 1] x [5, 3]







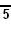



- A4xD2pxA1: [3, 3, 3] x [p] x [ ]













- C4xD2pxA1: [4, 3, 3] x [p] x [ ]













- F4xD2pxA1: [3, 4, 3] x [p] x [ ]













- G4xD2pxA1: [5, 3, 3] x [p] x [ ]













- B4xD2pxA1: [31, 1, 1] x [p] x [ ]







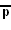



- A3xA3xA1: [3, 3] x [3, 3] x [ ]













- A3xC3xA1: [3, 3] x [4, 3] x [ ]













- A3xG3xA1: [3, 3] x [5, 3] x [ ]













- C3xC3xA1: [4, 3] x [4, 3] x [ ]













- C3xG3xA1: [4, 3] x [5, 3] x [ ]













- G3xA3xA1: [5, 3] x [5, 3] x [ ]













- A3xD2pxD2q: [3, 3] x [p] x [q]













- C3xD2pxD2q: [4, 3] x [p] x [q]













- G3xD2pxD2q: [5, 3] x [p] x [q]













- D2pxD2qxD2rA1: [p] x [q] x [r] x [ ]













- A7: [36]
8-hiperpluredroj (neplena)
redakti- A8: [3, 3, 3, 3, 3, 3, 3]















- C8: [4, 3, 3, 3, 3, 3, 3]















- B8: [31, 4, 1]













- E8: [34, 2, 1]













- A7xA1: [3, 3, 3, 3, 3, 3] x [ ]















- C7xA1: [4, 3, 3, 3, 3, 3] x [ ]















- B7xA1: [31, 3, 1] x [ ]













- [p, q, r, s, t] x [u]







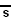

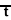





- [p, q, r, s] x [t, u]







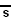



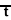



- [p, q, r] x [s, t, u]









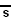

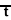



- [p, q, r, s] x [t] x [ ]







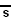



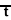



- [p, q, r] x [s, t] x [ ]









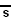

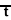



- [p, q, r] x [s] x [t]









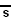



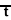

- [p, q] x [r, s] x [t]









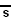



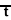

- [p, q] x [r] x [s] x [ ]











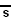



- [p] x [q] x [r] x [s]













 - kvarprismo
- kvarprismo
- A8: [3, 3, 3, 3, 3, 3, 3]
Specialaj okazoj
redaktiEn iuj specialaj okazoj la produtoj donas hiperkubojn:
- [ ] x [ ] = [4]



- [ ] x [ ] x [ ] = [4, 3]





- [ ] x [ ] x [ ] = [4, 3, 3]







- [ ] x [ ] x [ ] x [ ] = [4, 3, 3, 3]









- ...
Unuformaj hiperpluredroj ne konstrueblaj per konstruo de Wythoff
redaktiEkzistas unuformaj hiperpluredroj ne konstrueblaj per konstruo de Wythoff. Iuj el ili estas:
- En 3 dimensioj - nekonveksa granda durombo-dudek-dekduedro
- En 4 dimensioj - konveksa spacograndigita kontraŭprismo
- Ankaŭ iliaj karteziaj produtoj estas ne konstrueblaj per konstruo de Wythoff.
Vidu ankaŭ
redakti- Regula hiperpluredro
- Listo de regulaj hiperpluredroj
- Simbolo de Schläfli
- Plurlatero - 2-hiperpluredro
- Pluredro - 3-hiperpluredro
- Plurĉelo - 4-hiperpluredro
- 6-hiperpluredro
- 7-hiperpluredro
- 8-hiperpluredro
- 9-hiperpluredro
- 10-hiperpluredro
- Operacioj je hiperpluredroj kaj kahelaroj:
- Tranĉo t0, 1{p, ...}
- Laterotranĉo t0, 2{p, q, ...}
- Lateroverticotranĉo t0, 1, 2{p, q, ...}
- Edrotranĉo t0, 3{p, q, r, ...}
- Edroverticotranĉo t0, 1, 3{p, q, r, ...}
- Edrolaterotranĉo t0, 2, 3{p, q, r, ...}
- Edrolateroverticotranĉo t0, 1, 2, 3{p, q, r, ...}
- Ĉelotranĉo t0, 4{p, q, r, s, ...}
- Entutotranĉo t0, 1, ..., n-1{p1, p2, ..., pn-1}
- Rektigo t1{p, ...}
- Dutranĉo t1, 2{p, q, ...}
- Alternado
- Riproĉigo
- Simbolo de Schläfli - etendita simbolo de Schläfli priskribas rezultojn de la operacioj faritaj je regulaj hiperpluredroj kaj regulaj kahelaroj
Eksteraj ligiloj
redakti- George Olshevsky, Unuforma hiperpluredro en Glossary for Hyperspace.
- [1] Kalejdoskopoj: elektitaj skribaĵoj de H.S.M. Coxeter, 1995, ISBN 978-0-471-01003-6