Senpintigita kvaredro
La senpintigita kvaredro estas pluredro, arkimeda solido. Ĝi havas 4 regulajn seslaterajn edrojn, 4 regulajn triangulajn edrojn, 12 verticojn kaj 18 laterojn.
| Senpintigita kvaredro | |

| |

| |
| Klaku por rigardi turnantan bildon | |
| Vertica figuro | 3.6.6 |
| Bildo de vertico | 
|
| Bildo de reto | 
|
| Simbolo de Wythoff | 2 3 | 3 |
| Simbolo de Schläfli | t{3,3} |
| Figuro de Coxeter-Dynkin | |
| Indeksoj | U02 C16 W6 |
| Simbolo de Bowers | Tut |
| Verticoj | 12 |
| Lateroj | 18 |
| Edroj | 8 |
| Edroj detale | 4{3}+4{6} |
| χ | 2 |
| Geometria simetria grupo | Td |
| Duala | Trilateropiramidigita kvaredro |
| Bildo de duala | 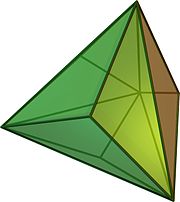
|
Areo kaj volumeno redakti
La areo A kaj la volumeno V de senpintigita kvaredro de latera longo a estas:
Karteziaj koordinatoj redakti
Karteziaj koordinatoj de la verticoj de senpintigita kvaredro centrita je (0, 0, 0) de latera longo estas ĉiuj permutoj de (±1,±1,±3) kun nepara kvanto de plusoj:
- (+3,+1,+1), (+1,+3,+1), (+1,+1,+3)
- (−3,−1,+1), (−1,−3,+1), (−1,−1,+3)
- (−3,+1,−1), (−1,+3,−1), (−1,+1,−3)
- (+3,−1,−1), (+1,−3,−1), (+1,−1,−3)
Aro de permutoj de (±1,±1,±3) donas verticojn de du intersekcantaj senpintigitaj kvaredroj (unuforma kombinaĵo de 2 senpintigitaj kvaredroj):
Vico de rilatantaj pluredroj kaj kahelaroj redakti
La senpintigita kvaredro estas ero de vico de senpintigitaj regulaj pluredroj kaj regulaj kahelaroj de la eŭklida kaj hiperbola ebenoj kun verticaj figuroj (3.2n.2n). .
| Triangula prismo (3.4.4) |
Senpintigita kvaredro (3.6.6) |
Senpintigita kubo (3.8.8) |
Senpintigita dekduedro (3.10.10) |
| Senpintigita seslatera kahelaro (3.12.12) |
Senpintigita seplatera kahelaro (3.14.14) |
Senpintigita oklatera kahelaro (3.16.16) |
Senpintigita naŭlatera kahelaro (3.18.18) |
Vidu ankaŭ redakti
Referencoj redakti
- Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)
Eksteraj ligiloj redakti
- Eric W. Weisstein, Senpintigita kvaredro en MathWorld.
- La unuformaj pluredroj
- Virtualaj realaj pluredroj - la enciklopedio de pluredroj
