Angulo

Angulo estas figuro formata de du strekoj etendantaj el punkto, la vertico de la angulo. Anguloj estas studataj en geometrio kaj trigonometrio.

Angulo de 45°.

Anguloj A kaj B estas apudaj. Ili formas komponitan angulon.

Historio kaj etimologio

la vorto angulo devenas el la Latina vorto angulus, kun la signifo de "angulo". Kognataj vortoj estas la greka ἀγκύλος (ankylοs) kun la signifo "kurba" kaj el ambaŭ pluraj variaĵoj en diversaj lingvoj, kiel la anglalingvaj vortoj "ankle" kaj "angle", la latinida hispanlingva "ángulo" ktp. Ĉiuj el ili estas konektataj kun la radiko el la prahindeŭropa radiko *ank-, kun la signifo "fleksi" aŭ "kliniĝi".

Eŭklido difinis ebenan angulon kiel la kliniĝo de unu al alia, en ebeno, de du linioj kiuj renkontiĝas kaj ne kuŝas rekte unu al la alia. Laŭ la novplatonisma metafizikisto Proklo, angulo devas esti aŭ kvalito, aŭ kvanto aŭ rilato. La unua koncepto, angulo kiel kvalito, estis utiligita fare de Eŭdemo de Rodoso, kiu rigardis angulon kiel devio de rekto; la dua, angulo kiel kvanto, estis utiligita fare de Karpo de Antioĥio, kiu rigardis ĝin kiel la intervalon aŭ spacon inter la intersekcantaj linioj; Eŭklido adoptis la trian: angulon kiel rilaton.

Identigi angulojn

En matematikaj esprimoj, estas komune uzi grekajn literojn (α, β, γ, θ, φ, . . . ) kiel variablojn indikantajn la grandecon de iu angulo (la simbolo π estas tipe ne uzita tiucele por eviti konfuzon kun la konstanto indikita per tiu simbolo). Oni uzas ankaŭ minusklajn latinajn literojn (a, b, c, . . . ). En kuntekstoj kie tio ne estas konfuza, angulo povas esti indikita per la majuskla latina litero indikanta sian verticon. Vidu la figurojn en ĉi tiu artikolo por ekzemploj.

Ankaŭ la tri difinaj punktoj povas identigi angulojn en geometriaj figuroj. Ekzemple, la angulo kun vertico A formita per la radioj AB kaj AC (t.e., la duonrektoj de punkto A tra punktoj B kaj C) estas indikita ∠BAC aŭ ${\widehat {\rm {BAC}}}$. Kie ekzistas neniu risko de konfuzo, la angulo foje povas esti referita per ununura vertico sole (en tiu kazo, "angulo A").

Alimaniere, angulo indikita kiel, ekzemple, ∠BAC povus rilati al iu ajn el kvar anguloj: la laŭhorloĝa (dekstruma) angulo de B ĝis C ĉirkaŭ A, la maldekstruma angulo de B ĝis C ĉirkaŭ A, la dekstruma angulo de C ĝis B ĉirkaŭ A, aŭ la maldekstruma angulo de C ĝis B ĉirkaŭ A, kie la direkto en kiu la angulo estas mezurita determinas ĝiajn signitajn angulojn. Tamen, en multaj geometriaj situacioj, estas evidente de la kunteksto ke la pozitiva angulo malpli ol aŭ egala al 180 gradoj estas signifita, kaj en tiuj kazoj, neniu ambigueco ekestas. Alie, por eviti ambiguecon, oni povas adopti specifajn konvenciojn tiel ke, ekzemple, ∠BAC ĉiam rilatas al la maldekstruma (pozitiva) angulo de B ĝis C ĉirkaŭ A kaj ∠CAB la maldekstruma (pozitiva) angulo de C ĝis B ĉirkaŭ A.

Mezuri angulojn

Angulilo dividita en centesimaj gradoj kaj amplitudo de 400^g.

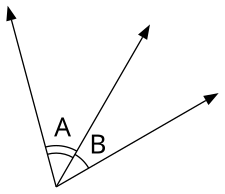
Por mezuri angulon, cirklo kun centro ĉe la vertico estu desegnita. La radiana mezuro de la angulo estas la longeco de la arko eltranĉita de la cirklo dividite per la longeco de la radiuso de la cirklo. La grada mezuro de la angulo estas la longeco de la arko dividite per la longeco de la cirkonferenco de la cirklo, kaj multiplikite per 360. La simbolo por gradoj estas superskribita cirkleto, kiel en 360°.

2π radianoj egalas al 360° (plena cirko), do unu radiano estas ĉirkaŭ 57° kaj unu grado estas π/180 radianoj.

Matematikistoj ĝenerale preferas la radianan mezuron, ĉar ĝi forigas la arbitreco de la nombro 360 de la grada sistemo kaj ĉar la trigonometriaj funkcioj havas pli simplajn tajlorajn seriojn se oni uzas la radianan sistemon. La SI-sistemo de unuoj uzas radianojn kiel (derivita) unuo de anguloj.

Radiano

La radiano (simbolo: rad) estas la angula mezurunuo en la Internacia sistemo de unuoj. Ĝi estas uzata ĉefe en trigonometrio kaj infinitezima kalkulo. Angulo inter du radiusoj de cirklo, arkolongo inter kiuj egalas al la radiuso, estas la ebena angulo.

En cirklo $l$ estas arkolongo, $r$ estas radiusolongo, $\alpha$ estas la larĝo de la angulo strekata de la arko, kaj $c$ estas cirklolongo:

$\alpha ^{\mathrm {rad} }={\frac {l}{r}}$

$l=r\cdot \alpha ^{\mathrm {rad} }$

Oni povas konverti gradojn al radianoj per ĉi tiu formulo:

$\alpha ^{\mathrm {rad} }={\frac {\pi }{180^{\circ }}}\cdot \alpha ^{(\circ )}$

Grado

Angulilo mezuras gradojn.

La grado estas angula mezurunuo kiu egalas al π / 180 radianoj, al naŭdekono de orto, aŭ al 10/9 gradusoj. La simbolo de grado estas °. Grado estas pli oportuna mezurunuo de angulo ol radiano, ĉar ĝi ebligas skribi multajn kutimajn angulojn (ekzemple orton) per entjera kvanto de gradoj. Por pli ĝusta mezuro de anguloj oni uzas aŭ dekumajn frakciojn de grado aŭ minutojn kaj sekundojn.

Angula minuto estas 1/60 de grado. Angula sekundo estas 1/60 de angula minuto, do 1/3600 de grado. La simbolo de angula minuto estas ' kaj la simbolo de angula sekundo estas ".

Ekzemplo: 34,863° ~= 34°51'47"

Ambaŭ notaciojn oni uzas por indiki la angulojn de geografiaj longitudo kaj latitudo, kiuj preskaŭ neniam estas indikataj per ne-gradaj unuoj.

Graduso

La indikilon de horloĝo kunformas diversajn tipojn de anguloj. En tiu okazo, akuta angulo.

La graduso (mallongigo: gr) ankaŭ nomita gono (simbolo: gon, el la greka gônia = "angulo") estas angula mezurunuo egala al π / 200 radianoj, al centono de orto, aŭ al 0,90 gradoj. La graduso estas la konsekvenco el la invento de la metro, ĉar la metro estas la 40.000.000-ono de la ter-ĉirkaŭo, kiam oni onigas tiun ĉirkaŭon per 400 gr, 1 km egalas al 1/100 da graduso. Pro tio, oni malbone komprenas ke oni ankoraŭ uzas la gradon en la aviadila kaj marveturada medioj kie la mezurunuoj estas la marmejlo (= 1 852 metroj) kaj la deksesonaj unuoj.

Nomo en Esperanto

Laŭ iuj, "graduso" en Esperanto ne nur estas mezurunuo por anguloj, sed ankaŭ por temperaturo, intenseco de tertremoj, vento-intenseco, kaj tiel plu. Laŭ la Plena Ilustrita Vortaro kaj PIV2, tamen, graduso estas nur mezurunuo por anguloj, egala al centono de orto. Ĉar orto egalas al 90 gradoj, unu graduso egalas al 0,9 gradoj.

En la rusa grado nomiĝas "градус" [gradus], kaj graduso nomiĝas "град" [grad].

Anguliloj

Angulilo estas instrumento por mezuri, difini, transporti aŭ streki angulon. Konsistas el cirkla aŭ duoncirkla disko kun angula skalo. La disko povas esti farita el plasto aŭ lado. Kutime la diametro estas inter 8 cm kaj 15 cm kun divido de 1° (grado) aŭ 0,5°. Por topografia mezurado ofte estas uzata skalo je gradusoj. Ofte anguliloj estas integritaj en trianguloj por desegnado. En metioj, kie plejofte ne necesas perfekta precizeco, por transporti kaj streki angulojn estas uzata alĝustebla angulilo.

• Anguliloj
• 
  Angulilo por 360°
• 
  Geotriangulo kun angulilo
• 
  Angulilo kun liniilo por lerneja uzo
• 
  Medicina angulilo
• 
  Elektronika angulilo
• 
  Alĝustebla angulilo

Dimensia analizo

Ebena angulo povas esti difinita kiel θ = s/r, kie θ estas la kvanto en radianoj de la koncerna angulo, s estas la longo de cirkla arko, kaj r estas radiuso. Unu radiano korespondas al la angulo por kiu s = r, tiel ke 1 radiano = 1 m/m = 1. Tamen, rad estas nur uzata por esprimi angulojn, ne por esprimi proporciojn de longoj ĝenerale. Simila kalkulado uzanta la areon de cirkla sektoro θ = 2A/r² havigas 1 radianon kiel 1 m²/m² = 1. La ŝlosila fakto estas, ke la radiano estas sendimensia unuo egala al 1. En SI 2019, la SI radiano estas difinita laŭ 1 rad = 1. Estas delonge establita praktiko en matematiko kaj tra ĉiuj areoj de scienco fari uzadon de rad = 1.

Giacomo Prando notis jene: "la nuna stato de aferoj kondukas neeviteble al fantomaj aperoj kaj malaperoj de la radiano en la dimensia analizo de fizikaj ekvacioj". Ekzemple, objekto pendanta de ŝnuro el pulio leviĝos aŭ falos je y = rθ centimetroj, kie r estas la grando de radiuso de la pulio en centimetroj kaj θ estas la grando de angulo tra kiu la pulio iĝas radianoj. Multobligante r per θ, la unuo radiano ne aperas en la produkto, nek la unuo-centimetro — ĉar ambaŭ faktoroj estas grandoj (nombroj). Simile en la formulo por la angula rapido de ruliĝanta rado, ω = v/r, radianoj aperas en la unuoj de ω, sed ne en la dekstra flanko. Anthony French nomas tiun fenomenon "porĉiama problemo en la instruado de mekaniko". Oberhofer diras ke la tipa konsilo ignori radianojn dum dimensia analizo kaj aldoni aŭ forigi radianojn en unuoj laŭ konvencio kaj kunteksta scio estas "pedagogie nekontentiga".

En 1993 la Metriko-Komisiono de la usona American Association of Physics Teachers (Unuiĝo de Fizik-Instruistoj) precizigis ke la radiano devus eksplicite aperi en kvantoj nur kiam malsamaj nombraj valoroj estus akiritaj kiam aliaj angulaj mezuroj estis uzitaj, kiel ekzemple en la kvantoj de angulmezuro (rad), angulrapideco (rad/s), angula akcelado (rad/s²), kaj torda rigideco (N⋅m/rad), kaj ne en la kvantoj de torko (N⋅m) kaj angula movokvanto (kg⋅m²/s).

Almenaŭ dekduo da sciencistoj inter 1936 kaj 2022 faris proponojn trakti la radianon kiel bazan mezurunuon por bazkvanto (kaj dimensio) de "ebena angulo". La revizio de Quincey de tiuj proponoj skizas du klasojn de propono. La unua eblo ŝanĝas la unuon de radiuso al metroj per radiano, sed tio estas malkongrua kun dimensia analizo por la areo de cirklo, πr². La alia eblo estas enkonduki dimensian konstanton. Laŭ Quincey tiu aliro estas "logike rigora" komparite kun SI, sed postulas "la modifon de multaj konataj matematikaj kaj fizikaj ekvacioj". Dimensia konstanto por angulo estas "sufiĉe stranga" kaj la malfacileco de modifado de ekvacioj por aldoni la dimensian konstanton verŝajne malebligas ĝeneraligitan uzon.

Aparte, Quincey identigas la proponon de Torrens enkonduki konstanton η egalan al 1 inversa radiano (1 rad⁻¹) en maniero simila al la enkonduko de la konstanto ε₀. Aliaj proponoj estas la mallongigo "rad" , la notacion $\langle \theta \rangle$ , kaj la konstantoj ם , ◁ , k , θ_C , kaj ${\cal {C}}={\frac {2\pi }{\Theta }}$ . Kun tiu ŝanĝo la formulo por la angulo subtenita en la centro de cirklo, s = rθ, estas modifita por iĝi s = ηrθ, kaj la Serio de Taylor por la sinuso de la angulo θ iĝas: $$\operatorname {Sin} \theta =\sin \ x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\eta \theta -{\frac {(\eta \theta )^{3}}{3!}}+{\frac {(\eta \theta )^{5}}{5!}}-{\frac {(\eta \theta )^{7}}{7!}}+\cdots ,$$ kie $x=\eta \theta =\theta /{\text{rad}}$ estas la angulo en radianoj.

La majuskla funkcio Sin estas la "kompleta" funkcio kiu prenas argumenton kun dimensio de angulo kaj estas sendependa de la unuoj esprimitaj, dum sin estas la tradicia funkcio sur puraj nombroj kiu supozas ke ĝia argumento estas sendimensia nombro en radianoj. La majuskla simbolo $\operatorname {Sin}$ povas esti indikita $\sin$ se estas klare ke la kompleta formo estas signifohava.

Nuna SI povas esti konsiderata relative al ĉi tiu kadro kiel natura unuosistemo kie la ekvacio η = 1 supozeble validas, aŭ simile, 1 rad = 1. Tiu radiana konvencio permesas la preterlason de η en matematikaj formuloj.

Difini radianon kiel bazunuon povas esti utila por softvaro, kie la malavantaĝo de pli longaj ekvacioj estas minimuma. Ekzemple, la biblioteko de Boost-unuoj difinas angulunuojn per dimensio ebena_angulo, kaj la unuosistemo de Mathematica simile konsideras angulojn kiel havantaj anguldimension.

Specoj de anguloj

Orta angulo.

Granda angulo.

Akuta (a), obtuza (b), kaj streĉita (c) anguloj. La akuta kaj obtuza anguloj estas konataj ankaŭ kiel oblikvaj anguloj.

Angulo de π/2 radianoj aŭ 90° (kvarono de plena cirklo) nomiĝas orta angulo. Anguloj pli malgrandaj ol orta angulo nomiĝas akuta angulo. Angulo pli granda ol orta angulo nomiĝas malakuta aŭ obtuza angulo.

Angulo de π radianoj aŭ 180° (duono de plena cirklo) nomiĝas streĉita angulo. Angulo malpli granda ol streĉita angulo nomiĝas konveksa angulo. Angulo pli granda ol streĉita angulo nomiĝas malkonveksa aŭ konkava angulo.

Suplementaj anguloj α kaj β : α+β=π

Suplementaj anguloj α kaj β : α+β=π

Komplementaj anguloj α kaj β : α+β=π/2

Vertikalaj anguloj α kaj β : α=β

Du anguloj estas nomataj komplementaj anguloj kiam ilia sumo egalas la ortan angulon, t.e. π/2 radianoj (aŭ 90°). Konsekvence, du komplementaj apudaj anguloj formas ortan angulon. Du komplementaj anguloj ne necese estas apudaj. Ekzemple en orta triangulo, la du anguloj apudaj al la hipotenuzo estas komplementaj, ĉar la sumo de ĉiuj anguloj de la triangulo estas π radianoj kaj la tria angulo egalas π/2 radianojn.

En cirklo, centra angulo estas angulo kies apekso (vertico) estas en la centro de la cirklo kaj kies du flankoj estas du radiusoj de cirklo. La grando de la angulo en radianoj egalas al la longo de la arko, kiun ĉi tiu angulo intersekcas de cirklo kies radiuso egalas 1. La grando de la centra angulo Θ estas 0° < Θ < 360 ° (notita en gradoj) aŭ 0 < Θ < 2π radianoj.

Galerio de anguloj

$0^{\circ }\,$	$15^{\circ }\,$	$30^{\circ }\,$	$45^{\circ }\,$	$60^{\circ }\,$	$75^{\circ }\,$
$90^{\circ }\,$	$105^{\circ }\,$	$120^{\circ }\,$	$135^{\circ }\,$	$150^{\circ }\,$	$165^{\circ }\,$
$180^{\circ }\,$	$195^{\circ }\,$	$210^{\circ }\,$	$225^{\circ }\,$	$240^{\circ }\,$	$255^{\circ }\,$
$270^{\circ }\,$	$285^{\circ }\,$	$300^{\circ }\,$	$315^{\circ }\,$	$330^{\circ }\,$	$345^{\circ }\,$
$360^{\circ }\,$

Pozitivaj kaj negativaj anguloj

En du-dimensia kartezia koordinata sistemo] angulo estas tipe difinita per ĝiaj du lateroj, kun ĝia vertico ĉe la origino. La komenca latero estas sur la pozitiva x-akso, dum la alia latero estas difinita per la mezuro de la komenca flanko en radianoj, gradoj aŭ turnoj. Kun pozitivaj anguloj reprezentantaj turnoj al la pozitiva y-akso kaj negativaj anguloj reprezentantaj turnoj al la negativa y-akso. Kiam karteziaj koordinatoj estas reprezentitaj per norma pozicio, difinitaj per la x-akso dekstre kaj la y-akso supren, pozitivaj rotacioj estas kontraŭhorloĝodirekte kaj negativaj rotacioj estas horloĝodirekte.

Konstruado de anguloj

Iuj anguloj estas konstrueblaj per rektilo kaj cirkelo. Tiuj estas la 90-grada, 60-grada, 72-grada kaj 54-grada kaj ĉiuj anguloj estigeblaj per duobligado, duonigado, adicio, aŭ subtraho de ili.

Por la anguloj $0^{\circ }<\alpha \leq 180^{\circ }$, proksimiĝa konstruo estas farebla per helpo de la Tria Teoremo de Tranĉataj Paralelaĵoj kombinata kun nombraj aksoj.

Konstruo de 90-grada angulo (orto)

Pli detalaj informoj troveblas en artikolo Orto.

La konstruo de 90-grada angulo rezultigas la rekton tra donita punkto P ortan al donita rekto $r$.

Konstruo je donita punkto ekster donita rekto (ortofaligo)

Konstruo je donita punkto sur donita rekto (t.e. donita rekto kaj vertico)

1. Desegnu cirklon ĉirkaŭ $P$ kun radiuso pli granda ol la proksimo de la punkto al la rekto. (Se la punkto $P$ estas sur la rekto $r$, la radiuso de la cirklo povas esti arbitra). Ĝi sekcas $r$ ĉe du punktoj.
2. Desegnu ĉirkaŭ ambaŭ sekcoj cirklon tiel, ke la du cirkloj sekcas unu la alian ĉe du punktoj.
3. Desegnu rekton tra la du sekcopunktoj de la novaj cirkloj. Tiu rekto sekcas $r$ orte kaj trairas $P$.

Ĉiutaga kaj figura senco

Angulo estas nefermita spaco limigita de du aŭ kelkaj sin reciproke renkontantaj surfacoj; ekzemple "La veturilo turnis angulen." En figura senco angulo estas malvasta, malofte vizitata aŭ rigardata loko. Angulo ankaŭ povas esti nedifinita loko ("la kvar anguloj de la tero").

Vidu ankaŭ

Cirkla sektoro A montrita en verda estas de radiuso r, angulo θ kaj longo L laŭ la cirkla perimetro

• Algebro
• Angulilo
• Arko
• Cirkla sektoro
• Duedra angulo
• Ebena angulo
• Grado
• Graduso
• Radiano
• Solida angulo
• Trigonometrio

Bibliografio

• Aboughantous, Charles H. (2010), A High School First Course in Euclidean Plane Geometry, Universal Publishers, ISBN 978-1-59942-822-2
• Brinsmade, J. B. (Decembro 1936). "Plane and Solid Angles. Their Pedagogic Value When Introduced Explicitly". American Journal of Physics. 4 (4): 175–179. Bibcode:1936AmJPh...4..175B. doi:10.1119/1.1999110.
• Brownstein, K. R. (Julio 1997). "Angles—Let's treat them squarely". American Journal of Physics. 65 (7): 605–614. Bibcode:1997AmJPh..65..605B. doi:10.1119/1.18616.
• Chisholm, Hugh, eld. (1911), "Angle", Encyclopædia Britannica, vol. 2 (11a eld.), Cambridge University Press, p. 14
• Gilles Cohen (dir.), Les angles sous tous les angles, Bibliothèque Tangente , Numéro 53, Editions Pôle Paris, 2015, (rete) [1].
• [2] [descartes.cnice.mec.es]. Descartes. Konsultita la 27an de Novembro 2017.
• Eder, W E (Januaro 1982). "A Viewpoint on the Quantity "Plane Angle"". Metrologia. 18 (1): 1–12. Bibcode:1982Metro..18....1E. doi:10.1088/0026-1394/18/1/002. S2CID 250750831.
• Foster, Marcus P (1a de Decembro 2010). "The next 50 years of the SI: a review of the opportunities for the e-Science age". Metrologia. 47 (6): R41 – R51. doi:10.1088/0026-1394/47/6/R01. S2CID 117711734.
• Heiberg, Johan Ludvig (1908), Heath, T. L. (eld.), Euclid, The Thirteen Books of Euclid's Elements, vol. 1, Cambridge: Cambridge University Press.
• Leonard, B P (1a de Oktobro 2021). "Proposal for the dimensionally consistent treatment of angle and solid angle by the International System of Units (SI)". Metrologia. 58 (5): 052001. Bibcode:2021Metro..58e2001L. doi:10.1088/1681-7575/abe0fc. S2CID 234036217.
• Lévy-Leblond, Jean-Marc (Septembro 1998). "Dimensional angles and universal constants". American Journal of Physics. 66 (9): 814–815. Bibcode:1998AmJPh..66..814L. doi:10.1119/1.18964.
• Mills, Ian (1a de Junio 2016). "On the units radian and cycle for the quantity plane angle". Metrologia. 53 (3): 991–997. Bibcode:2016Metro..53..991M. doi:10.1088/0026-1394/53/3/991. S2CID 126032642.
• Mohr, Peter J; Phillips, William D (1a de Februaro 2015). "Dimensionless units in the SI". Metrologia. 52 (1): 40–47. arXiv:1409.2794. Bibcode:2015Metro..52...40M. doi:10.1088/0026-1394/52/1/40.
• Mohr, Peter J; Shirley, Eric L; Phillips, William D; Trott, Michael (23a de Junio 2022). "On the dimension of angles and their units". Metrologia. 59 (5): 053001. arXiv:2203.12392. Bibcode:2022Metro..59e3001M. doi:10.1088/1681-7575/ac7bc2.
• Quincey, Paul (1a de Aprilo 2016). "The range of options for handling plane angle and solid angle within a system of units". Metrologia. 53 (2): 840–845. Bibcode:2016Metro..53..840Q. doi:10.1088/0026-1394/53/2/840. S2CID 125438811.
• Quincey, Paul (1a de Oktobro 2021). "Angles in the SI: a detailed proposal for solving the problem". Metrologia. 58 (5): 053002. arXiv:2108.05704. Bibcode:2021Metro..58e3002Q. doi:10.1088/1681-7575/ac023f. S2CID 236547235.
• Real Academia de Ciencias Exactas, Física y Naturales, eld. (1999). Diccionario esencial de las ciencias. Espasa. ISBN 84-239-7921-0.
• Romain, Jacques E. (Julio 1962). "Angle as a fourth fundamental quantity". Journal of Research of the National Bureau of Standards Section B. 66B (3): 97. doi:10.6028/jres.066B.012.
• Slocum, Jonathan (2007), Preliminary Indo-European lexicon — Pokorny PIE data, University of Texas research department: linguistics research center, arkivita el la originalo la 27an de Junio 2010, Alirita la 2an de Februsro 2010
• Torrens, A B (1a de Januaro 1986). "On Angles and Angular Quantities". Metrologia. 22 (1): 1–7. Bibcode:1986Metro..22....1T. doi:10.1088/0026-1394/22/1/002. S2CID 250801509.
• David A. Wallis, «History of Angle Measurement», en Proceedings, FIG Workshop Week 2005 & 8th International Conference on the Global Spatial Data Infrastructure, Kairo, aprilo 2005 [3] Konsultita la 27an de Novembro 2017.

Eksteraj ligiloj

• [4] Arkivigite je 2005-03-23 per la retarkivo Wayback Machine
• [5] Arkivigite je 2006-02-08 per la retarkivo Wayback Machine Angulo
• [6]
• [7] Arkivigite je 2006-06-28 per la retarkivo Wayback Machine
• Ausstellung „Historische Winkelmesser“
• [8]

Fontoj

•   Angulo en ReVo .