Seslatera kahelaro
En geometrio, la seslatera kahelaro estas kahelaro de la eŭklida ebeno, konsistanta el seslateroj. Ĝia subspeco estas la regula seslatera kahelaro, konsistanta el regulaj seslateroj kaj havanta simbolon de Schläfli t0{6,3} aŭ t2{3,6}.
| Regula seslatera kahelaro | |

| |

| |
| Vertica figuro | 6.6.6 |
| Bildo de vertico | 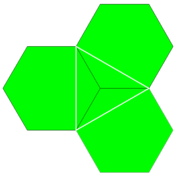
|
| Simbolo de Wythoff | 3 | 6 2 2 6 | 3 3 3 3 | |
| Simbolo de Schläfli | {6,3} t{3,6} |
| Figuro de Coxeter-Dynkin | |
| Simbolo de Bowers | Hexat |
| Geometria simetria grupo | p6m |
| Duala | Triangula kahelaro |
| Bildo de duala | 
|
Propraĵoj de regula formo
redaktiLa ena angulo de la regula seslatero estas 120 gradoj, tiel tri seslateroj je punkto havas plenan angulon de 360 gradoj. Regula seslatera kahelaro estas unu el tri regulaj kahelaroj de la eŭklida ebeno. La aliaj du estas la kvadrata kahelaro kaj la regula triangula kahelaro.
Unuformaj kolorigoj
redaktiEstas 3 diversaj unuformaj kolorigoj de regula seslatera kahelaro. La koloroj estu priskribataj per ciferoj 1, 2, 3. Tiam en la 3 variantoj de la kolorigoj, la 3 seslateroj ĉirkaŭ ĉiu vertico havas kolorojn 111, 112, 123.
| Bildo | Simbolo de Wythoff | Geometria simetria grupo |
|---|---|---|
| 3 | 6 2 | *p632 (p6m) | |
| 2 6 | 3 | *p632 (p6m) | |
| 3 3 3 | | *333 (p3) |
Vicoj de rilatantaj pluredroj kaj kahelaroj
redaktiLa regula seslatera kahelaro estas ero de vico de regulaj pluredroj kaj regulaj kahelaroj de la eŭklida kaj hiperbola ebenoj kun verticaj figuroj (n3) aŭ (n.n.n).
| Kvaredro (33) |
Kubo (43) |
Dekduedro (53) |
| Seslatera kahelaro (63) |
Ordo-3 seplatera kahelaro (73) |
Ordo-3 oklatera kahelaro (83) |
La regula seslatera kahelaro estas ero de vico de regulaj pluredroj kaj regulaj kahelaroj de la eŭklida kaj hiperbola ebenoj kun verticaj figuroj (n.6.6).
| Senpintigita kvaredro (3.6.6) |
Senpintigita okedro (4.6.6) |
Senpintigita dudekedro (5.6.6) |
| Seslatera kahelaro (6.6.6) |
Ordo-7 senpintigita triangula kahelaro (7.6.6) |
(8.6.6) |
Kahelaroj konstruitaj surbaze
redaktiEstas 8 unuformaj kahelaroj kiu povas esti konstruitaj surbaze de la regula seslatera kahelaro (aŭ ĝia duala triangula kahelaro), inkluzive la seslateran kahelaron mem.
El la 8 formoj nur 7 kiu estas topologie diversaj, ĉar la senpintigita triangula kahelaro estas topologie identa al la seslatera kahelaro.
En la bildoj la edroj bazitaj je la originalaj edroj estas kolorigita kiel ruĝaj, bazitaj je la la originalaj lateroj estas bluaj, bazitaj je la originalaj verticoj estas flavaj.
| Kahelaro | Operacio aplikita | Simbolo de Schläfli | Simbolo de Wythoff | Vertica konfiguro | Bildo |
|---|---|---|---|---|---|
| Seslatera kahelaro | La originala formo | t0{6,3} | 3 | 6 2 | 63 | |
| Senpintigita seslatera kahelaro | Senpintigo | t0,1{6,3} | 2 3 | 6 | 3.12.12 | |
| Rektigita seslatera kahelaro (tri-seslatera kahelaro) |
Rektigo | t1{6,3} | 2 | 6 3 | (3.6)2 | |
| Dutranĉita seslatera kahelaro (senpintigita triangula kahelaro) |
Dutranĉo | t1,2{6,3} | 2 6 | 3 | 6.6.6 | |
| Duala seslatera kahelaro (triangula kahelaro) |
Dualigo | t2{6,3} | 6 | 3 2 | 36 | |
| Laterotranĉita seslatera kahelaro (malgranda rombo-tri-seslatera kahelaro) |
Laterotranĉo | t0,2{6,3} | 6 3 | 2 | 3.4.6.4 | |
| Entutotranĉita seslatera kahelaro (granda rombo-tri-seslatera kahelaro) |
Entutotranĉo aŭ lateroverticotranĉo | t0,1,2{6,3} | 6 3 2 | | 4.6.12 | |
| Riproĉa seslatera kahelaro | Riproĉigo | s{6,3} | | 6 3 2 | 3.3.3.3.6 |
Neregulaj formoj
redaktiLa regula seslatera kahelaro povas esti malformita al la aliaj geometriaj proporcioj kaj malsamaj simetrioj. Ekzemple, la norma brika ŝablono povas esti konsiderata kiel neregula seslatera kahelaro. Ĉiu ortangula briko havas 4 verticojn je la anguloj kaj 2 verticojn en la longaj randoj, dividantajn ĉiun el ili je du samliniaj lateroj.
Uzoj
redaktiĈi tiu seslatera ŝablono ekzistas en naturo en abelia ĉelaro.
Ekzemploj:
Vidu ankaŭ
redakti- Seslatera krado
- Seslatera prisma kahelaro
- Kahelaro de 2-dimensia ebeno
- Listo de unuformaj ebenaj kahelaroj
- Listo de regulaj hiperpluredroj
- Plurformo de regula seslatero - subaro de seslateroj el la seslatera kahelaro
Referencoj
redakti- Branko Grünbaum, Shephard G. C.. (1987) Tilings and Patterns - Kahelaroj kaj ŝablonoj. Novjorko: W. H. Freeman. ISBN 0-7167-1193-1. (Ĉapitro 2.1: Regulaj kaj unuformaj kahelaroj, p. 58-65)
- Robert Williams, La geometria fundamento de natura strukturo: Fonta libro de dizajno, Novjorko, Dovero, 1979, p35.
