Senpintigita kubo
(Alidirektita el Senpintigita sesedro)
La senpintigita kubo aŭ senpintigita sesedro estas pluredro, arkimeda solido. Ĝi havas 6 regulajn oklaterajn edrojn, 8 regulajn triangulajn edrojn, 24 verticojn kaj 36 laterojn.
| Senpintigita kubo | |
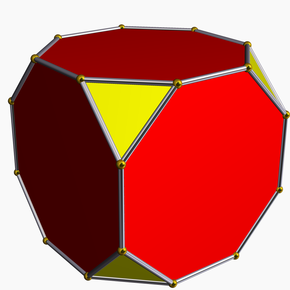
| |

| |
| Klaku por rigardi turnantan bildon | |
| Vertica figuro | 3.8.8 |
| Bildo de vertico | 
|
| Bildo de reto | 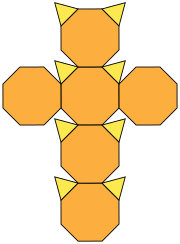
|
| Simbolo de Wythoff | 2 3 | 4 |
| Simbolo de Schläfli | t{4,3} |
| Figuro de Coxeter-Dynkin | |
| Indeksoj | U09 C21 W8 |
| Simbolo de Bowers | Tic |
| Verticoj | 24 |
| Lateroj | 36 |
| Edroj | 14 |
| Edroj detale | 8{3}+6{8} |
| χ | 2 |
| Geometria simetria grupo | Oh |
| Duala | Trilateropiramidigita okedro |
| Bildo de duala | 
|
Areo kaj volumeno
redaktiLa areo A kaj la volumeno V de senpintigita kubo de latera longo a estas:
Karteziaj koordinatoj
redaktiKarteziaj koordinatoj de verticoj de senpintigita kubo centrita je (0, 0, 0):
- (±ξ, ±1, ±1),
- (±1, ±ξ, ±1)
- (±1, ±1, ±ξ)
kie ξ = .
Rilatantaj pluredroj
redaktiLa senpintigita kubo ekzistas en la aro de senpintigitaj formoj inter kubo kaj okedro:
| Kubo | Senpintigita kubo | Kubokedro | Senpintigita okedro | Okedro |
Ĝi komunigas sian situon de verticoj kun tri stelaj unuformaj pluredroj:
| Granda rombo-sesedro (4.8/3.4/3.8/5) |
Granda kubokubo-okedro (8/3.3.8/3.4) |
Unuforma granda rombokub-okedro (4.3/2.4.4) |
Solidoj de Johnson surbaze de la senpintigita kubo estas:
| Pligrandigita senpintigita kubo (J66) | Dupligrandigita senpintigita kubo (J67) |
La senpintigita kubo estas ero de vico de senpintigitaj regulaj pluredroj kaj regulaj kahelaroj de la eŭklida kaj hiperbola ebenoj kun verticaj figuroj (3.2n.2n).
| Triangula prismo (3.4.4) |
Senpintigita kvaredro (3.6.6) |
Senpintigita kubo (3.8.8) |
Senpintigita dekduedro (3.10.10) |
| Senpintigita seslatera kahelaro (3.12.12) |
Senpintigita seplatera kahelaro (3.14.14) |
Senpintigita oklatera kahelaro (3.16.16) |
Senpintigita naŭlatera kahelaro (3.18.18) |
| Kombinaĵo de 5 senpintigitaj kuboj |
Referencoj
redakti- Williams, Robert. (1979) The Geometrical Foundation of Natural Structure: A Source Book of Design - La Geometria Fundamento de Natura Strukturo: Fonta Libro de Dizajno. Dover Publications, Inc. ISBN 0-486-23729-X. (Sekcio 3-9)
Eksteraj ligiloj
redakti- Eric W. Weisstein, Senpintigita kubo en MathWorld.
- La unuformaj pluredroj
- Virtualaj realaj pluredroj - la enciklopedio de pluredroj
