Funkcio (matematiko)
| Ĉi tiu artikolo temas pri funkcio en matematiko. Por parto de programo rigardu la paĝon Subprogramo. |
| Matematikaj funkcioj |
|---|
| fonta aro, cela aro • bildo, malbildo • bildaro, argumentaro |
| Fundamentaj funkcioj |
| Algebraj funkcioj: konstanta • lineara • kvadrata • polinoma • racionala • Transformo de Möbius Aliaj funkcioj: trigonometriaj • inversa trigonometria • hiperbola • eksponenta • logaritma • potenca |
| Specialaj funkcioj |
| erara • β • Γ • ζ • η • W de Lambert • de Bessel |
| Nombroteoriaj funkcioj: |
| τ • σ • de Möbius • φ • π • λ |
| Ecoj: |
| totaleco kaj parteco • pareco kaj malpareco • monotoneco • bariteco • periodeco • disĵeteco • surĵeteco • dissurĵeteco kontinueco • derivaĵeco • integralebleco |
En matematiko, funkcio estas duvalenta rilato, kiu rilatigas al membroj de unu aro po ne pli ol unu elemento el alia (aŭ la sama) aro.

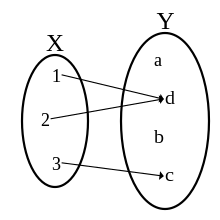


Ĉi tio estas tre ĝenerala koncepto aperanta en ĉiuj areoj de matematiko kaj aliaj sciencoj. La funkcio estas uzata, interalie, kiel ilo por esprimi interdependecon (situacio, en kiu du variabloj estas interdependaj) kaj, kiel tia, permesas formalan prezenton de la naturo de interdependeco inter malsamaj grandoj en la kampoj de scienco, inĝenierado kaj ekonomiko.
Formalaj difinoj
redaktiX kaj Y estu aroj. Oni diras, ke funkcio f ĵetas X al Y, simbole
se f estas tia rilato super , ke por ĉiu en f ekzistas ne pli ol unu duopo ; en tia okazo oni skribas .
La aron X oni nomas la fonta aro; la aron Y, la cela aro, simbole iam E(f).
La aron de ĉiuj valoroj de funkcio f oni nomas ĝia bildaro, simbole iam Im(f) (mallongigo de la anglalingva vorto image), kaj la aron de ĉiuj x en X, por kiuj f estas difinita, oni nomas ĝia malbildo aŭ argumentaro, simbole iam Dom(f) aŭ D(f) (mallongigo de la samsenca anglalingva termino domain).
Funkcioj ĉieaj kaj partaj
redaktiKutime (sed ne ĉiam) la malbildo de funkcio koincidas kun la tuta aro X, t.e. ĝia malbildo koincidas kun ĝia fonta aro. Tia funkcio nomiĝas ĉie difinita, totala aŭ ĉiea.
En kuntekstoj, kie oni konsideras funkciojn ne nepre ĉie difinitajn, oni ofte uzas la terminon partaj funkcioj por klare atentigi, ke oni ne supozu, ke ĉiuj funkcioj en la koncerna diskurso nepre estas totalaj, kiel ofte okazas.
Multaj klasoj de funkcioj kutimaj en matematika praktiko enhavas partajn funkciojn. Tipa grava ekzemplo estas la klaso de racionalaj funkcioj.
Aliflanke, en matematikaj tekstoj la aŭtoroj (ofte sen eksplicita atentigo) uzas la terminon "funkcio" jen en la senco ĉie difinita funkcio, jen en la senco funkcio ne nepre ĉie difinita. En ĉiu konkreta kunteksto la leganto devas konscii pri tio, kiun sencon adoptis la aŭtoro, eĉ se tio ne estas eksplicite klarigite.
Terminuzo
redaktiOni tradicie uzas la terminon funkcio, se la aroj X kaj Y estas nombraj; en okazoj pli ĝeneralaj oni fojfoje uzas ankaŭ la terminojn ĵeto, transformo aŭ bildigo. Speciale kiam X = Y, oni ofte nomas funkcion transformo.
Variabloj
redaktiLa notacion y = f(x) oni nomas funkcia notacio, kie x estas sendependa variablo, kaj y - dependa variablo.
- Sendependa variablo (la argumento) - la variablo, por ĉiu el kies unuopa valoro povas ekzisti (sola) responda valoro de funkcio.
- Dependa variablo (la rezulto) - la variablo donita per la valoroj de la funkcio; ekz. en la funkcio y = sin(x), x - estas la sendependa variablo (argumento), dum y estas dependa variablo.
Formoj de prezento
redaktiLa rilaton, kiu konsistigas la funkcion, oni povas prezenti kiel regulon determinantan rezulton por ĉiu argumento. La rimedoj por esprimi la regulon povas esti diversaj:
- Tabela - per la vicoj de argumentoj kaj ĝiaj konformaj signifoj;
- Grafika - la ordigitaj paroj (x, y), kiuj formas la funkcion, povas esti presentita kiel punktoj M(x, y) de la kartezia sistemo por vidigi la grafikaĵon, en la formo de la linio;
-
Grafikaĵo de funkcio.
- Analitika - per egalaĵa formulo, ekz. y = 3x² + 1.
Tipoj de funkcioj
redakti- Funkcio difinita sur ordohava aro (aro provizita per parta ordo) estas kreskanta, se por ajnaj elementoj de la aro x₁ < x₂ validas malegalaĵo f(x₁) < f(x₂). Se por x₁ < x₂, veras la alia malegalaĵo f(x₁) > f(x₂), la funkcio nomiĝas malkreskanta. Ekzemple, funkcio y=x² estas malkreskanta en la intervalo ]-∞;0] kaj estas kreskanta en la intervalo [0;+∞[.
- Funkcio estas para, se ĝia argumentaro D estas simetria rilate al 0 kaj por ajna x ∈ D(f) validas egalaĵo f(-x) =f(x). Kaj ĝi nomiĝas malpara, se validas egalaĵo f(-x) = -f(x). Ekzemple, la funkcio y=x² estas para, kaj la funkcioj y=x kaj y=x³ estas malparaj.
- Funkcio estas perioda kun periodo p, kiu ne egalas al 0, se por ajna x ∈ D(f) la nombroj x-p kaj x+p ankaŭ apartenas al D(f) kaj veras la egalaĵo: f(x+p) = f(x), ankaŭ f(x) = f(x-p) kaj f(x) = f(x+kp), kie k estas entjero.
- Funkcio estas konveksa, se D(f) estas konveksa aro kaj por ajnaj x kaj y el D(f) kaj t ∈ [0;1] estas vera la neegalaĵo :
-
Konveksa funkcio estas kontinua sur D(f) se D(f) estas malferma intervalo, aŭ ĝenerale malferma konveksa subaro de Rn.
- identa funkcio bildigas ĉiun elementon de iu aro al ĝi mem.
- Formale: Por ajna aro A, la identa funkcio de A, nomata aŭ , estas funkcio tia ke por ĉiu x en A.
- La identa funkcio estas dissurĵeto kaj estas sia propra inverso:
- La identa funkcio estas neŭtrala elemento de la funkcia komponaĵo: Por ajna funkcio validas:
- inversa funkcio al funkcio , estas funkcio , por kiu komponaĵo kun funkcio f estas identa funkcio:
- por ĉiuj x ∈ X kaj
- por ĉiuj y ∈ Y
Ekzemploj kaj malekzemploj
redakti- La rilato, kiu rilatigas ĉiun personon kun ties aĝo, estas funkcio de la aro de homoj al la aro de naturaj nombroj, ĉar ĉiu persono havas ununuran aĝon.
- La rilato, kiu rilatigas ĉiun reelan nombron kun ĝia kvadrato, estas funkcio de la aro de reelaj nombroj al ĝi mem. Ĝi povas esti priskribita jene:
- La rilato, kiu rilatigas ĉiun personon kun la lando, en kiu li estas civitano, ne estas funkcio, ĉar ekzistas homoj kun pluraj civitanecoj.
- La rilato, kiu rilatigas ĉiun personon kun ties oficiala ŝakrango, estas parta sed ne ĉiea/totala funkcio, ĉar ekzistas homoj, kiuj ne estas rangitaj de FIDE aŭ alia ŝak-organizaĵo.
Gravaj specoj de funkcioj
redaktiKontinua funkcio estas funkcio, kies valoro malmulte ŝanĝiĝas en okazo de malgranda ŝanĝo de la argumento. Se malgranda ŝanĝo de la argumento povas produkti rompan salton en valoro de la funkcio, la funkcio estas nekontinua. La ĉirkaŭteksto de ĉi tiu termino estas reelo-valoraj funkcioj sur la reela domajno aŭ sur topologia aŭ metrika spacoj escepte la kompleksajn nombrojn. Pri komplekso-valoraj funkcioj vidu artikolon kompleksa analitiko. La rimarkinda diferenco en maniero estas tiu ke en la reela domajno, la punktoj en la domajno kiuj estas punktoj de nekontinueco estas specialaĵoj. Sed en la kompleksa domajno tiaj punktoj estas kutime aparte forprenitaj el la domajno, do la funkcio kontinua en kompleksa domajno estas kontinua sur malkonektita partoj de reela domajno.
Lineara funkcio estas matematika esprimo kun du malsamaj signifoj. Unuflanke, ĝi povas esti ĉiu funkcio de la formo
- .
Tia funkcio reprezentas konstantan kreskon de rilate al . La grafikaĵo de tia funkcio estas ĉiam rekta linio. Se , tiam estas kreskanta funkcio; se , ĝi estas malkreskanta; kaj se , tiam estas konstanta funkcio. Derivaĵo de lineara funkcio je ĝia sendependa variablo x, egalas al la konstanto m. La problemo kun la supre skizita signifo de lineara funkcio estas, ke tia funkcio ne estas lineara transformo. Tial multaj matematikistoj nomas tian funkcion afina funkcio, kaj rezervas la esprimon lineara funkcio por linearaj transformoj.
Polinoma funkcio estas funkcio difinita per polinomo. Polinomo estas esprimo, en kiu konstantoj kaj variabloj estas kombinitaj uzante nur adiciojn, subtrahojn kaj multiplikojn. Polinomo povas esti prezentita kiel sumo de termoj. Tiel,
estas polinomo de grado 6 kun tri variabloj (x, y, z), sed
ne estas polinomo. Polinomaj funkcioj estas grava klaso de glataj funkcioj; vorto glata signifas, ke ili estas malfinie diferencialeblaj, t.e. ke ili havas derivaĵojn de ĉiu finia ordo. Pro ilia simpla strukturo, polinomoj estas facile kalkuleblaj, kaj estas ofte uzataj en cifereca analitiko por polinoma interpolado aŭ por ciferece integrali pli komplikajn funkciojn.
Eksponenta funkcio, aŭ eksponencialo, estas unu de la plej gravaj funkcioj en matematiko. Ĝi estas skribita kiel exp(x) aŭ ex, kie e egalas proksimume al 2.71828183 kaj estas la bazo de la naturaj logaritmoj. Kiel funkcio de la reela variablo x, la grafikaĵo de ex estas ĉiam pozitiva (super la absciso (x-akso)) kaj rapide pligrandiĝas por x>0. Inversa funkcio de eksponenta funkcio, la natura logaritmo, ln(x), estas difinita por ĉiuj pozitivaj x.
Vidu ankaŭ
redakti- Grafikaĵo
- Elipsa funkcio
- Kontinua funkcio
- Lineara funkcio
- Polinoma funkcio
- Eksponenta funkcio
- Trigonometria funkcio
- Speciala funkcio
- Nulo de funkcio
- Disĵeta funkcio
- Surĵeta funkcio
- Dissurĵeta funkcio
- Bijekcio
Eksteraj ligiloj
redakti- http://functions.wolfram.com
- http://archives.math.utk.edu/visual.calculus Arkivigite je 2006-01-28 per la retarkivo Wayback Machine
- http://math.hws.edu/xFunctions
- http://geography.about.com/library/misc/bl2capitals.htm
- http://archive.numdam.org/article/CM_1954-1956__12__81_0.pdf La kanonaj formoj de la 2, 3, 4 -dimensiaj paraanalitikaj funkcioj]. Far M. R. Fréchet, en Esperanto, en Revuo Compositio Mathematica, 12 (1954-1956), p. 81-96, formo PDF.